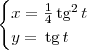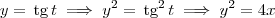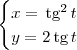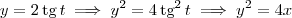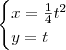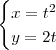Claudin escreveu:Alguém conseguiu chegar no resultado como o gabarito? Ainda não consegui compreender.
Primeiro vamos analisar uma parametrização para a parábola

.
Na figura abaixo, desejamos relacionar as coordenadas do ponto C = (x0, y0) da parábola com o ângulo
t. Esse ângulo será o nosso parâmetro.
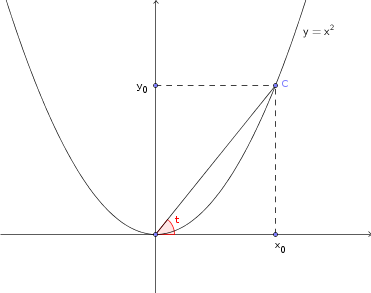
- figura1.png (6.04 KiB) Exibido 4185 vezes
Do triângulo retângulo formado na figura, podemos dizer que:
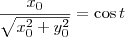
Lembrando que (x0, y0) é um ponto da parábola, podemos dizer que

. Temos então que:
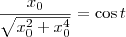


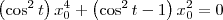
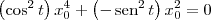
![\left[\left(\cos^2 t\right) x_0^2 - \,\textrm{sen}^2\, t \right]x_0^2 = 0 \left[\left(\cos^2 t\right) x_0^2 - \,\textrm{sen}^2\, t \right]x_0^2 = 0](/latexrender/pictures/36f378826e63d9169ae06d62187e1677.png)
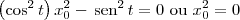
Resolvendo essa equações, obtemos que
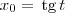
ou
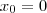
.
Lembando que

, temos que
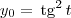
ou

.
Desse modo, considerando
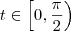
podemos obter as seguintes equações paramétricas para o "lado direito" da parábola:
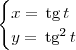
Utilizando um desenvolvimento análogo ao que foi feito para esse caso, podemos concluir que considerando
![t\in \left(\frac{\pi}{2}, \pi\right] t\in \left(\frac{\pi}{2}, \pi\right]](/latexrender/pictures/a87757804020e851a25a8dd3e87fbaec.png)
as equações paramétricas para o "lado esquerdo" da parábola também serão essas.
Considerando então tudo que foi discutido até aqui, fica fácil perceber que a parábola

pode ter equações paramétricas dadas por:
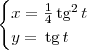
Esta é uma resposta válida para o exercício. Conferindo a resposta, note que:
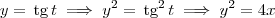
Mas também podemos usar um pouco mais de álgebra (e criatividade) para escrever outras equações paramétricas:
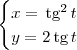
Veja que essa também é uma resposta válida:
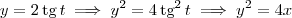
Para finalizar a discussão, mudando o parâmetro usado também existem outras respostas válidas:
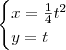
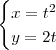
Nesses casos o parâmetro
t não está relacionado com um ângulo, mas sim com a coordenada y dos pontos da parábola.





 , x é dado por:
, x é dado por:

 , substituir x por t e encontrar y.
, substituir x por t e encontrar y.



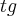 envolvida, ai não sei como chegar na resposta correta.
envolvida, ai não sei como chegar na resposta correta.




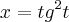
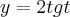


 .
.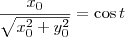
 . Temos então que:
. Temos então que: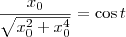


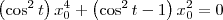
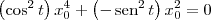
![\left[\left(\cos^2 t\right) x_0^2 - \,\textrm{sen}^2\, t \right]x_0^2 = 0 \left[\left(\cos^2 t\right) x_0^2 - \,\textrm{sen}^2\, t \right]x_0^2 = 0](/latexrender/pictures/36f378826e63d9169ae06d62187e1677.png)
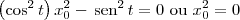
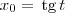 ou
ou 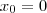 .
. , temos que
, temos que 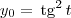 ou
ou  .
.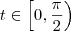 podemos obter as seguintes equações paramétricas para o "lado direito" da parábola:
podemos obter as seguintes equações paramétricas para o "lado direito" da parábola: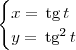
![t\in \left(\frac{\pi}{2}, \pi\right] t\in \left(\frac{\pi}{2}, \pi\right]](/latexrender/pictures/a87757804020e851a25a8dd3e87fbaec.png) as equações paramétricas para o "lado esquerdo" da parábola também serão essas.
as equações paramétricas para o "lado esquerdo" da parábola também serão essas. pode ter equações paramétricas dadas por:
pode ter equações paramétricas dadas por: