Determine o valor da seguinte equação:
![\sqrt[3]{5*\sqrt[3]{3*\sqrt[3]{5*\sqrt[3]{3*\sqrt[3]{5}*\sqrt[3]{3}}}}} \sqrt[3]{5*\sqrt[3]{3*\sqrt[3]{5*\sqrt[3]{3*\sqrt[3]{5}*\sqrt[3]{3}}}}}](/latexrender/pictures/f7a1816b5620819327e74f115005b767.png)
a)
![\sqrt[8]{375} \sqrt[8]{375}](/latexrender/pictures/abe338419fe6786a69f9a42d8f447540.png)
b)
![\sqrt[3]{35} \sqrt[3]{35}](/latexrender/pictures/0da97b0b34b25b27206e705c7c0a1a40.png)
c)
![\sqrt[3]{53} \sqrt[3]{53}](/latexrender/pictures/0fd61278ff8260c5aa158d236e577df5.png)
d)
![\sqrt[6]535} \sqrt[6]535}](/latexrender/pictures/ebe3a214458a61643cbdb933fa155791.png)
Gabarito letra a
Como chegar a esse resultado?

![\sqrt[3]{5*\sqrt[3]{3*\sqrt[3]{5*\sqrt[3]{3*\sqrt[3]{5}*\sqrt[3]{3}}}}} \sqrt[3]{5*\sqrt[3]{3*\sqrt[3]{5*\sqrt[3]{3*\sqrt[3]{5}*\sqrt[3]{3}}}}}](/latexrender/pictures/f7a1816b5620819327e74f115005b767.png)
![\sqrt[8]{375} \sqrt[8]{375}](/latexrender/pictures/abe338419fe6786a69f9a42d8f447540.png)
![\sqrt[3]{35} \sqrt[3]{35}](/latexrender/pictures/0da97b0b34b25b27206e705c7c0a1a40.png)
![\sqrt[3]{53} \sqrt[3]{53}](/latexrender/pictures/0fd61278ff8260c5aa158d236e577df5.png)
![\sqrt[6]535} \sqrt[6]535}](/latexrender/pictures/ebe3a214458a61643cbdb933fa155791.png)

![5\sqrt[3]{3.\sqrt[3]{5}.\sqrt[3]{3}} ===> 5\sqrt[3]{3.\sqrt[3]{5}.\sqrt[3]{3}} ===>](/latexrender/pictures/3a4e6052e5596eab2ef9b8040c95ee79.png)
![\sqrt[3]{5^3.3.\sqrt[3]{3.5}} ====> \sqrt[3]{5^3.3.\sqrt[3]{3.5}} ====>](/latexrender/pictures/deb933a215a44518e448470bd054c220.png)
![\sqrt[3]{\sqrt[3]{5^9.3^3.3.5}} ====> \sqrt[3]{\sqrt[3]{5^9.3^3.3.5}} ====>](/latexrender/pictures/8db1a16cafd7620d949f753467cfec5b.png)
![\sqrt[9]{3^4.5^{10}} \sqrt[9]{3^4.5^{10}}](/latexrender/pictures/48394296579d0bac86175133792a8821.png)
![3.\sqrt[3]{\sqrt[9]{3^4.5^{10}}} ====> 3.\sqrt[3]{\sqrt[9]{3^4.5^{10}}} ====>](/latexrender/pictures/18ecabe5b1f61695f19ad0582ecee2cb.png)
![3.\sqrt[27]{3^4.5^{10}} ====> 3.\sqrt[27]{3^4.5^{10}} ====>](/latexrender/pictures/98f7855da373083f4fbaf770758a6f88.png)
![\sqrt[27]{3^{27}.3^4.5^{10}} ====> \sqrt[27]{3^{27}.3^4.5^{10}} ====>](/latexrender/pictures/aef37b551f7e439fd56269254fd6164c.png)
![\sqrt[27]{3^{31}.5^{10}} \sqrt[27]{3^{31}.5^{10}}](/latexrender/pictures/187a4d1e8e0eb4b735ed89639e0c4788.png)
![5.\sqrt[3]{\sqrt[27]{3^{31}.5^{10}}} ====> 5.\sqrt[3]{\sqrt[27]{3^{31}.5^{10}}} ====>](/latexrender/pictures/607644ce033fd3fc0dcfe04bb5db2018.png)
![5.\sqrt[81]{3^{31}.5^{10}} ====> 5.\sqrt[81]{3^{31}.5^{10}} ====>](/latexrender/pictures/7c1f140d34041e6984e45bdeeca8797f.png)
![\sqrt[81]{5.^{81}.3^{31}.5^{10}} ====> \sqrt[81]{5.^{81}.3^{31}.5^{10}} ====>](/latexrender/pictures/2d7e6436494f94cc48e156ba97aad3f3.png)
![\sqrt[81]{5^{91}.3^{31}} \sqrt[81]{5^{91}.3^{31}}](/latexrender/pictures/7b1bda653109eacabf548b58ce00003d.png)
![\sqrt[3]{\sqrt[81]{5^{91}.3^{31}}} ====> \sqrt[3]{\sqrt[81]{5^{91}.3^{31}}} ====>](/latexrender/pictures/b3f063a0dee70f4cd0b7e936a443cb53.png)
![\sqrt[243]{5^{91}.3^{31}} ====> \sqrt[243]{5^{91}.3^{31}} ====>](/latexrender/pictures/0c1c30a50a3fccc60e941ce570e91d8a.png) devo ter errado alguma passagem, mas não consigo notar.
devo ter errado alguma passagem, mas não consigo notar.

Carlso Dargo escreveu:Questão 12
Determine o valor da seguinte equação:
a)
b)
c)
d)
Gabarito letra a
Como chegar a esse resultado?
Carlso Dargo escreveu:eu esqueci de colocar uma '...' no final ok!
![\sqrt[3]{5\sqrt[3]{3\sqrt[3]{5\sqrt[3]{3\sqrt[3]{5\sqrt[3]{3\ldots}}}}}} \sqrt[3]{5\sqrt[3]{3\sqrt[3]{5\sqrt[3]{3\sqrt[3]{5\sqrt[3]{3\ldots}}}}}}](/latexrender/pictures/809807bf2c232c3314b7f6d77617e770.png)
![L = \sqrt[3]{5\sqrt[3]{3\sqrt[3]{5\sqrt[3]{3\sqrt[3]{5\sqrt[3]{3\ldots}}}}}} L = \sqrt[3]{5\sqrt[3]{3\sqrt[3]{5\sqrt[3]{3\sqrt[3]{5\sqrt[3]{3\ldots}}}}}}](/latexrender/pictures/dee483c787602b0f73d3d6b7590cba31.png)
![L = \sqrt[3]{5\sqrt[3]{3L}} L = \sqrt[3]{5\sqrt[3]{3L}}](/latexrender/pictures/4db308f7d6d933c51f85b56cd7688db0.png)
![L^3 = 5\sqrt[3]{3L} L^3 = 5\sqrt[3]{3L}](/latexrender/pictures/f05ea3362737390770f06e2c896d859d.png)
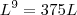
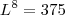
![L = \sqrt[8]{375} L = \sqrt[8]{375}](/latexrender/pictures/332dd14e2109b8ed40559019830bce75.png)


Carlso Dargo escreveu:Não Luiz Aquino, no texto é usada a palavra equação
Carlso Dargo escreveu:e ela está exatamente da forma como postada,faltava apenas a "..."
![\sqrt[3]{5}\cdot \sqrt[3]{3} \sqrt[3]{5}\cdot \sqrt[3]{3}](/latexrender/pictures/0a612ccc2954fa9828d1b490b8a5353d.png) ao invés de
ao invés de ![\sqrt[3]{5\cdot \sqrt[3]{3}} \sqrt[3]{5\cdot \sqrt[3]{3}}](/latexrender/pictures/644c1abde3bfb3ea34f5144ad30dfe52.png) . Então além das reticências, provavelmente também há essa correção.
. Então além das reticências, provavelmente também há essa correção.Carlso Dargo escreveu:Trata-se de uma progressão geometrica infinita.
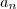 é o n-ésimo termo dessa sequência, então temos que:
é o n-ésimo termo dessa sequência, então temos que:![a_n = \sqrt[3]{5\sqrt[3]{3a_{n-1}}} a_n = \sqrt[3]{5\sqrt[3]{3a_{n-1}}}](/latexrender/pictures/78d23764d0df1fe1ee4066c0c621200b.png)
![a_n = \sqrt[3]{\sqrt[3]{375a_{n-1}}} a_n = \sqrt[3]{\sqrt[3]{375a_{n-1}}}](/latexrender/pictures/bde801dac7b489ed295ca793b17d1f40.png)
![a_n = \sqrt[9]{375a_{n-1}} a_n = \sqrt[9]{375a_{n-1}}](/latexrender/pictures/0225ce91dc000bafa8d34a70f10ae489.png)
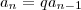 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
