 por Suellen » Seg Abr 16, 2012 19:30
por Suellen » Seg Abr 16, 2012 19:30
De um ponto A no solo, visam-se a base B e o topo C de um bastão colocado verticalmente no alto de uma colina, sob um ângulo de 30º e 45º, respectivamente. Se o bastão mede 4 m de comprimento, a altura da colina, em metros, é igual a:
![a)\sqrt[]{3}
b)2
c)2\sqrt[]{3}
d)2(\sqrt[]{3}+1)
e)2(\sqrt[]{3}+3) a)\sqrt[]{3}
b)2
c)2\sqrt[]{3}
d)2(\sqrt[]{3}+1)
e)2(\sqrt[]{3}+3)](/latexrender/pictures/f603eb4d5f036bf84aaaaecea4c93ea9.png)
a resposta é a letra d) só que eu quero saber como que resolve por favor?
-
Suellen
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 12, 2012 22:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Ter Abr 17, 2012 22:04
por fraol » Ter Abr 17, 2012 22:04
Boa noite,
Segue figura ilustrativa:
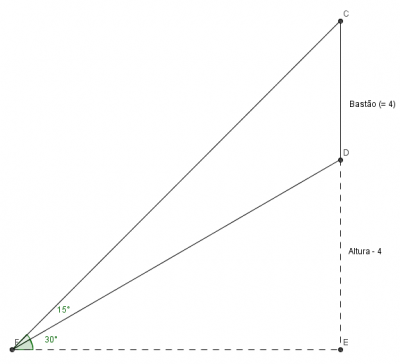
- figura
Na figura temos:
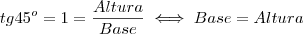
Na figura temos:
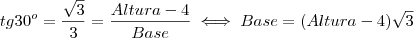
Igualando as duas expressões temos:
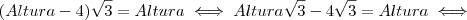
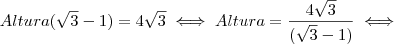
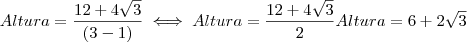
E finalmente:
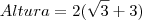
Veja que esse resultado não bate com o gabarito dado.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por fraol » Qua Abr 18, 2012 11:00
por fraol » Qua Abr 18, 2012 11:00
Boa dia,
Estive pensando sobre a divergência entre a solução que postei antes e o gabarito e cheguei a conclusão que interpretei erradamente o enunciado.
Na figura que apresentei você deve considerar o
trecho DE como sendo a Altura da colina.
Alterando de acordo com a nova abordagem:
Na figura temos:
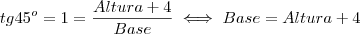
Na figura temos:
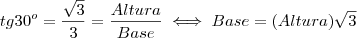
Igualando as duas expressões temos:
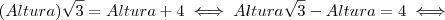
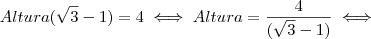
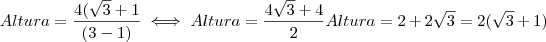
Assim sendo o gabarito apresentado está correto.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Suellen » Qua Abr 25, 2012 20:23
por Suellen » Qua Abr 25, 2012 20:23
obg pela resposta.
só não entendi as duas ultimas linhas da sua segunda resposta
-
Suellen
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 12, 2012 22:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Qui Abr 26, 2012 15:40
por fraol » Qui Abr 26, 2012 15:40
Boa tarde vou adicionar os passos intermediários nas duas linhas finais, veja:
Na figura temos:
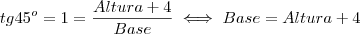
Na figura temos:
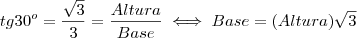
Igualando as duas expressões temos:
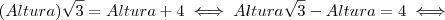
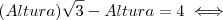
, agora colocaremos Altura em evidência
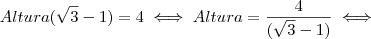
, aqui levamos
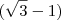
para o segundo membro com a operação inversa .
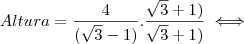
com esta multiplicação obtemos uma diferença de quadrados no denominador que tem como resultado o quadrado do primeiro termo menos o quadrado do segundo termo, assim:
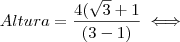
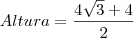
, neste passo efetuamos a multiplicação no numerador e a diferença no denominador.
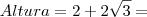
, aqui dividimos por 2 e
finalmente, colocamos o 2 em evidência e obtemos
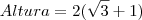
.
.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por Suellen » Qui Mai 03, 2012 17:55
por Suellen » Qui Mai 03, 2012 17:55
Agora sim eu entendi tudo!
Mt obg pela paciência

Boa tarde
-
Suellen
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qui Abr 12, 2012 22:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3598 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5277 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- trigonometria
por Cleyson007 » Qua Set 24, 2008 19:44
- 2 Respostas
- 3419 Exibições
- Última mensagem por admin

Ter Set 30, 2008 19:08
Trigonometria
-
- trigonometria
por Micheline » Dom Jan 25, 2009 16:21
- 5 Respostas
- 4972 Exibições
- Última mensagem por Cleyson007

Seg Jan 26, 2009 17:27
Trigonometria
-
- Trigonometria
por Flavio » Sex Fev 13, 2009 21:29
- 5 Respostas
- 5134 Exibições
- Última mensagem por Molina

Seg Fev 16, 2009 01:53
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![a)\sqrt[]{3}
b)2
c)2\sqrt[]{3}
d)2(\sqrt[]{3}+1)
e)2(\sqrt[]{3}+3) a)\sqrt[]{3}
b)2
c)2\sqrt[]{3}
d)2(\sqrt[]{3}+1)
e)2(\sqrt[]{3}+3)](/latexrender/pictures/f603eb4d5f036bf84aaaaecea4c93ea9.png)

![a)\sqrt[]{3}
b)2
c)2\sqrt[]{3}
d)2(\sqrt[]{3}+1)
e)2(\sqrt[]{3}+3) a)\sqrt[]{3}
b)2
c)2\sqrt[]{3}
d)2(\sqrt[]{3}+1)
e)2(\sqrt[]{3}+3)](/latexrender/pictures/f603eb4d5f036bf84aaaaecea4c93ea9.png)

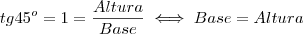
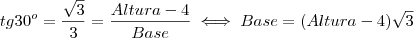
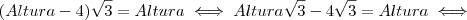
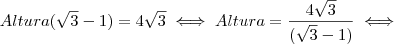
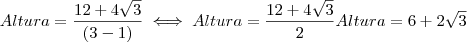
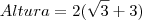

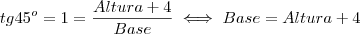
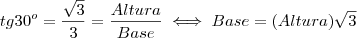
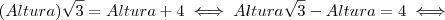
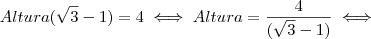
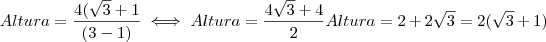


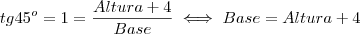
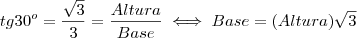
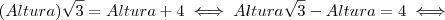
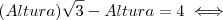 , agora colocaremos Altura em evidência
, agora colocaremos Altura em evidência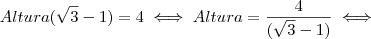 , aqui levamos
, aqui levamos 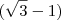 para o segundo membro com a operação inversa .
para o segundo membro com a operação inversa .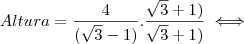 com esta multiplicação obtemos uma diferença de quadrados no denominador que tem como resultado o quadrado do primeiro termo menos o quadrado do segundo termo, assim:
com esta multiplicação obtemos uma diferença de quadrados no denominador que tem como resultado o quadrado do primeiro termo menos o quadrado do segundo termo, assim: 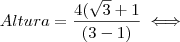
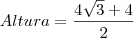 , neste passo efetuamos a multiplicação no numerador e a diferença no denominador.
, neste passo efetuamos a multiplicação no numerador e a diferença no denominador.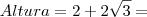 , aqui dividimos por 2 e
, aqui dividimos por 2 e 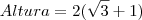 .
.






