 por souzalucasr » Qui Abr 05, 2012 11:36
por souzalucasr » Qui Abr 05, 2012 11:36
Olá pessoal,
Fiz uma prova ontem e fiquei em dúvida na seguinte questão:
Calcule o limite a seguir:
![\lim_{x\rightarrow0}\frac{\sqrt[3]{x}-1}{x^2-x} \lim_{x\rightarrow0}\frac{\sqrt[3]{x}-1}{x^2-x}](/latexrender/pictures/ca45b28898898b7f78ed8763982cd50b.png)
Utilizei a equivalência

, de forma a obter

=

=

cancelando os termos

no denominador e numerador, obtive

Foi exatamente nesse ponto em que "travei". Ao entregar a prova, perguntei ao professor como poderia resolver e ele me disse que seria pela análise do sinal, mas não sei bem o que isso quer dizer e como fazer. Vocês poderiam me ajudar?
Muito obrigado!
Essa é minha primeira postagem aqui
-
souzalucasr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Abr 05, 2012 11:21
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Economia
- Andamento: cursando
 por MarceloFantini » Qui Abr 05, 2012 12:30
por MarceloFantini » Qui Abr 05, 2012 12:30
O limite é com
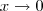
mesmo? Se já viram limites infinitos, a resposta sai de cara da primeira linha, pois o numerador tende a menos um e o denominador para zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por souzalucasr » Qui Abr 05, 2012 13:01
por souzalucasr » Qui Abr 05, 2012 13:01
Eu não estou com a prova em mãos, mas tenho 99% de certeza que é x tendendo a 0, pois houve esse comentário do professor quanto ao "estudo do sinal". Eu faltei a essa aula, por isso estou perdido. Além disso, não encontrei nada no livro. Segunda-feira vou só confirmar se é isso mesmo, mas até lá vou tentando resolver.
Obrigado!
-
souzalucasr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Abr 05, 2012 11:21
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Economia
- Andamento: cursando
 por LuizAquino » Qui Abr 05, 2012 19:11
por LuizAquino » Qui Abr 05, 2012 19:11
souzalucasr escreveu:Calcule o limite a seguir:
![\lim_{x\rightarrow0}\frac{\sqrt[3]{x}-1}{x^2-x} \lim_{x\rightarrow0}\frac{\sqrt[3]{x}-1}{x^2-x}](/latexrender/pictures/ca45b28898898b7f78ed8763982cd50b.png)
souzalucasr escreveu:Utilizei a equivalência

, de forma a obter

=

=

cancelando os termos

no denominador e numerador, obtive

Foi exatamente nesse ponto em que "travei". Ao entregar a prova, perguntei ao professor como poderia resolver e ele me disse que seria pela análise do sinal, mas não sei bem o que isso quer dizer e como fazer. Vocês poderiam me ajudar?
A dica sobre a "análise do sinal" é devido ao fato desse limite ter como resultado

.
Como já disse o colega
MarceloFantini, analisando a expressão original do limite, note que o numerador tende para -1 e o denominador para 0. Isso já é um indício que temos um limite cujo o resultado é

. Falta agora saber se é
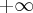
ou

. Para saber disso precisamos analisar o sinal.
Para x próximo de 0, temos que o numerador é negativo (como já vimos, ele tende para -1).
Precisamos agora analisar o sinal do denominador quando x está próximo de 0. Isso significa que precisamos analisar o sinal da função
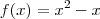
quando x está próximo de zero. Fazendo o estudo do sinal dessa função polinomial do segundo grau, percebemos que f(x) tende para 0 por valores positivos, quando x tende a 0 pela esquerda. Por outro lado, f(x) tende para 0 por valores negativos, quando x tende a 0 pela direita.
Em resumo:
(i) quando x tende a 0 pela esquerda, o numerador é negativo e o denominador é positivo;
(ii) quando x tende a 0 pela direita, o numerador é negativo e o denominador é negativo;
Conclusão:
![\lim_{x\to 0^-} \frac{\sqrt[3]{x} - 1}{x^2 - x} = -\infty \lim_{x\to 0^-} \frac{\sqrt[3]{x} - 1}{x^2 - x} = -\infty](/latexrender/pictures/cd763d09f9c46589bb78e54b5bf3d3db.png)
![\lim_{x\to 0^+} \frac{\sqrt[3]{x} - 1}{x^2 - x} = +\infty \lim_{x\to 0^+} \frac{\sqrt[3]{x} - 1}{x^2 - x} = +\infty](/latexrender/pictures/ca23a7c9df3111da51374883cda55923.png)
Como esses limites laterais são diferentes, temos que
não existe o limite
![\lim_{x\to 0} \frac{\sqrt[3]{x} - 1}{x^2 - x} \lim_{x\to 0} \frac{\sqrt[3]{x} - 1}{x^2 - x}](/latexrender/pictures/ea17b159bfcabc8a50c0338778963f42.png)
.
souzalucasr escreveu:Eu não estou com a prova em mãos, mas tenho 99% de certeza que é x tendendo a 0, pois houve esse comentário do professor quanto ao "estudo do sinal". Eu faltei a essa aula, por isso estou perdido. Além disso, não encontrei nada no livro.
Eu gostaria de recomendar que você assista a videoaula "05. Cálculo I - Limites Infinitos". Ela está disponível em meu canal no YouTube:
http://www.youtube.com/LCMAquino
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por souzalucasr » Sex Abr 06, 2012 11:50
por souzalucasr » Sex Abr 06, 2012 11:50
Muito obrigado, Luiz e Marcelo!
Entendi perfeitamente agora. As aulas do youtube serão muito úteis. Vou continuar resolvendo o máximo de exercícios que puder e, quando tiver alguma dúvida, posto aqui para tentar aprender um pouco mais.
[]s
-
souzalucasr
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Abr 05, 2012 11:21
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Economia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- derivada análise de sinal
por JoaoLuiz07 » Seg Fev 08, 2016 16:26
- 1 Respostas
- 1333 Exibições
- Última mensagem por adauto martins

Qua Fev 10, 2016 12:31
Cálculo: Limites, Derivadas e Integrais
-
- limite com sinal infinito
por SILMARAKNETSCH » Sex Nov 09, 2012 16:05
- 4 Respostas
- 2387 Exibições
- Última mensagem por MarceloFantini

Seg Nov 12, 2012 10:57
Cálculo: Limites, Derivadas e Integrais
-
- Empacada por um sinal
por Fernanda Lauton » Sex Jul 02, 2010 10:08
- 5 Respostas
- 2668 Exibições
- Última mensagem por Fernanda Lauton

Sáb Jul 03, 2010 22:28
Logaritmos
-
- Estudo do sinal
por victorleme » Dom Mai 08, 2011 16:33
- 1 Respostas
- 2926 Exibições
- Última mensagem por Molina

Dom Mai 08, 2011 17:08
Polinômios
-
- Função ( Estudo do sinal )
por clara » Dom Jun 21, 2009 20:55
- 1 Respostas
- 5329 Exibições
- Última mensagem por Molina

Seg Jun 22, 2009 12:57
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow0}\frac{\sqrt[3]{x}-1}{x^2-x} \lim_{x\rightarrow0}\frac{\sqrt[3]{x}-1}{x^2-x}](/latexrender/pictures/ca45b28898898b7f78ed8763982cd50b.png)
 , de forma a obter
, de forma a obter =
=  =
= 
 no denominador e numerador, obtive
no denominador e numerador, obtive 


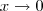 mesmo? Se já viram limites infinitos, a resposta sai de cara da primeira linha, pois o numerador tende a menos um e o denominador para zero.
mesmo? Se já viram limites infinitos, a resposta sai de cara da primeira linha, pois o numerador tende a menos um e o denominador para zero.

 .
.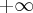 ou
ou  . Para saber disso precisamos analisar o sinal.
. Para saber disso precisamos analisar o sinal.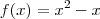 quando x está próximo de zero. Fazendo o estudo do sinal dessa função polinomial do segundo grau, percebemos que f(x) tende para 0 por valores positivos, quando x tende a 0 pela esquerda. Por outro lado, f(x) tende para 0 por valores negativos, quando x tende a 0 pela direita.
quando x está próximo de zero. Fazendo o estudo do sinal dessa função polinomial do segundo grau, percebemos que f(x) tende para 0 por valores positivos, quando x tende a 0 pela esquerda. Por outro lado, f(x) tende para 0 por valores negativos, quando x tende a 0 pela direita.![\lim_{x\to 0^-} \frac{\sqrt[3]{x} - 1}{x^2 - x} = -\infty \lim_{x\to 0^-} \frac{\sqrt[3]{x} - 1}{x^2 - x} = -\infty](/latexrender/pictures/cd763d09f9c46589bb78e54b5bf3d3db.png)
![\lim_{x\to 0^+} \frac{\sqrt[3]{x} - 1}{x^2 - x} = +\infty \lim_{x\to 0^+} \frac{\sqrt[3]{x} - 1}{x^2 - x} = +\infty](/latexrender/pictures/ca23a7c9df3111da51374883cda55923.png)
![\lim_{x\to 0} \frac{\sqrt[3]{x} - 1}{x^2 - x} \lim_{x\to 0} \frac{\sqrt[3]{x} - 1}{x^2 - x}](/latexrender/pictures/ea17b159bfcabc8a50c0338778963f42.png) .
.




