N consegui realizar por teorema de tales!

[bmachado]

Uma reta paralela ao lado BC de um triangulo ABC determina sobre o lado AB segmentos de 3cm e de 12cm. Calcule as medidas dos segmentos que essa reta determina sobre o lado AC, cuja medida e 10cm. Obrigado

[LuizAquino]

Uma reta paralela ao lado BC de um triangulo ABC determina sobre o lado AB segmentos de 3cm e de 12cm. Calcule as medidas dos segmentos que essa reta determina sobre o lado AC, cuja medida e 10cm.

A figura abaixo ilustra o exercício.

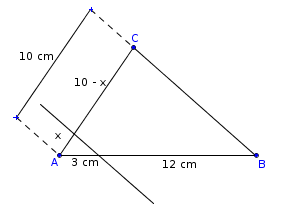
figura.png (4.49 KiB) Exibido 5810 vezes

Com base nessa figura, por favor informe qual foi a sua dificuldade em aplicar o Teorema de Tales.

[bmachado]

Uma reta paralela ao lado BC de um triangulo ABC determina sobre o lado AB segmentos de 3cm e de 12cm. Calcule as medidas dos segmentos que essa reta determina sobre o lado AC, cuja medida e 10cm.

A figura abaixo ilustra o exercício.

figura.png

Com base nessa figura, por favor informe qual foi a sua dificuldade em aplicar o Teorema de Tales.

Obrigado e pq n consegui visualizar o desenho dessa forma, entao, fiz errado, vlw

[educosta]

Como o triângulo menor formado pela reta que passa pelo lado AB é um triângulo retângulo, pode-se calcular o cateto oposto ao ângulo de 30 graus utilizando o seno do ângulo, com este valor calculado, basta diminuir da medida de 10cm para se obter o valor dos segmentos formados sobre o lado AC.

[bmachado]

Como o triângulo menor formado pela reta que passa pelo lado AB é um triângulo retângulo, pode-se calcular o cateto oposto ao ângulo de 30 graus utilizando o seno do ângulo, com este valor calculado, basta diminuir da medida de 10cm para se obter o valor dos segmentos formados sobre o lado AC.

Obrigado pela atencao, pois, sou graduado há anos na area de saude, e resolvi fazer outro curso q exige no vestibular da matematica, ta osso!Mas aproveitando estou c duvida na resoluca de uma questao q envolve tg, vc sabe sobre esse assunto, chegue a questao no link tem a resolucao, obrigado; Na figura, ACB é reto, ABD = DBC = ?,
AD = x, DC = 1 e BC = 3.Com as informações dadas, determine o valor
de x.

A pergunta eu postei ontem em:http://www.ajudamatematica.com/viewtopic.php?f=119&t=7666
Obrigado

[LuizAquino]

Como o triângulo menor formado pela reta que passa pelo lado AB é um triângulo retângulo, pode-se calcular o cateto oposto ao ângulo de 30 graus utilizando o seno do ângulo, com este valor calculado, basta diminuir da medida de 10cm para se obter o valor dos segmentos formados sobre o lado AC.

Não há triângulo retângulo algum nessa figura.