Na figura abaixo, ABCD é um quadrado, os pontos M e N são médios dos lados BC e CD, respectivamente, e P é o ponto de interseção dos segmentos AM e BN.
(a imagem do problema esta em http://imageshack.us/photo/my-images/193/quadradoa.jpg)
A razão PM/PA é igual a:
A) 5
B) 2(5)^1/2
C) 4
D) 3
E) (5)^1/2
Pelo gabarito seria letra C (resposta: 4).
***********************************************************************************
Eu só encontro 3...
Estou calculando da seguinte forma:
No triangulo ABP
tg30 = (3^1/2)/3
igualei isso a z/x
achei z=(x(3)^1/3)/3
No triangulo PMB
tg 30 = (3^1/2)/3 = y/((x(3)^1/2))/3
achei x=3y
PA/PM = x/y = 3y/y = 3
Nao sei onde estou errando...
Grata,
Julia



 .
.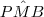 é compartilhado pelos triângulos ABM e BPM.
é compartilhado pelos triângulos ABM e BPM.