Claudin escreveu:Já conheço o programa sim.
Ok.
Claudin escreveu:Mas na hora da prova eu não terei esse programa (...)
Isso é verdade. Mas enquanto você estiver estudando, pode utilizar o programa para conferir a sua resposta.
Em uma de suas mensagens, você perguntou:
Claudin escreveu:A inversa seria?
5 4 35
-2 -3 -14
1 2 6
Note que você poderia utilizar o programa para conferir isso. Ou ainda, você mesmo poderia conferir manualmente a sua resposta fazendo a seguinte multiplicação:
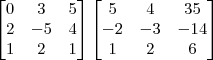
Se essa multiplicação resultar na matriz identidade, então a inversa foi calculada corretamente. Caso contrário, algum erro foi cometido.
Vale lembrar que na hora da prova você também não terá a sua disposição esse fórum para pedir ajuda. É recomendado que você aprenda a conferir a sua resposta manualmente.
Claudin escreveu:(...) por isso gostaria de ver o desenvolvimento para ajudar a entender.
Foi o que eu sempre tentei mostrar isso aqui no Fórum.
Continuo sem compreender como resolver
Na sua primeira mensagem, você perguntou:
Claudin escreveu:Porém pelo método de Gauss Jordan, como iniciarei o escalonamento sendo que a¹¹ = 0 ?
Não tem como passar ele para 1, para que comece o escalonamento.
E ai oq eu faço?
Em seguida, você comentou:
Claudin escreveu:Cheguei em um resultado muito estranho, está errado, vou refazer, se alguém postar o início do desenvolvimento já ajuda.
Depois disso, eu mostrei para você o início assim como você pediu:
Comece fazendo a operação
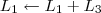
:
![\left[\begin{array}{ccc|ccc} 0 & 3 & 5 & 1 & 0 & 0 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \left[\begin{array}{ccc|ccc} 0 & 3 & 5 & 1 & 0 & 0 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right]](/latexrender/pictures/0300efe2f869d7ff98c3bd10e5f5c0e9.png)
Entretanto, você ainda continua com dúvidas. Eu vou então continuar os passos.
2º Passo)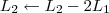
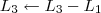
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right]](/latexrender/pictures/d56718e58c14e6be4a675798d0b2c218.png) 3º Passo)
3º Passo)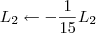
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right]](/latexrender/pictures/bf92d321716c471edd90a6d9d4a9323d.png) 4º Passo)
4º Passo)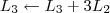
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right]](/latexrender/pictures/8bbd6a7495d616b3577aeb425fd217a5.png) 5º Passo)
5º Passo)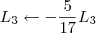
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/a18e87a70e18a740ac1a1e48d3e9a375.png) 6º Passo)
6º Passo)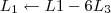
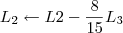
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/61fdfca5f5d28b7cf66be0a778fedbbb.png) 7º Passo)
7º Passo)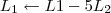
![\left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & -\frac{13}{51} & \frac{7}{51} & \frac{37}{51} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & -\frac{13}{51} & \frac{7}{51} & \frac{37}{51} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/95113ef6e8f4c96b29789121f4cc76a3.png)
Podemos então reescrever a resposta final como:
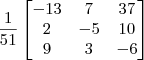
Para conferir o resultado, basta efetuar a operação:
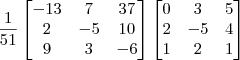
Note que o resultado dessa operação será a matriz identidade.
ObservaçãoSe você deixasse para transformar os pivôs em 1 apenas no final do processo (como expliquei em
seu outro tópico), você iria economizar tempo realizando menos operações com frações.


 .
.

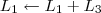 :
:![\left[\begin{array}{ccc|ccc}
0 & 3 & 5 & 1 & 0 & 0 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right] \sim \left[\begin{array}{ccc|ccc}
1 & 5 & 6 & 1 & 0 & 1 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right] \left[\begin{array}{ccc|ccc}
0 & 3 & 5 & 1 & 0 & 0 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right] \sim \left[\begin{array}{ccc|ccc}
1 & 5 & 6 & 1 & 0 & 1 \\
2 & -5 & 4 & 0 & 1 & 0 \\
1 & 2 & 1 & 0 & 0 & 1
\end{array}\right]](/latexrender/pictures/10ad4caffa4ade108485e7c9f4a66be8.png)
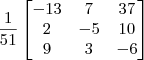
![\left[\begin{array}{ccc|ccc}
1 & 0 & 0 & \frac{67}{3} & \frac{56}{3} & -9 \\
0 & 1 & 0 & \frac{34}{3} & \frac{11}{3} & \frac{-20}{3} \\
0 & 0 & 1 & 3 & 1 & -2
\end{array}\right] \sim \left \left[\begin{array}{ccc|ccc}
1 & 0 & 0 & \frac{67}{3} & \frac{56}{3} & -9 \\
0 & 1 & 0 & \frac{34}{3} & \frac{11}{3} & \frac{-20}{3} \\
0 & 0 & 1 & 3 & 1 & -2
\end{array}\right] \sim \left](/latexrender/pictures/a8f7ef10416b77057eb890f47cd3c40b.png)
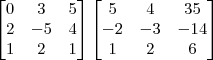
![\left[\begin{array}{ccc|ccc} 0 & 3 & 5 & 1 & 0 & 0 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \left[\begin{array}{ccc|ccc} 0 & 3 & 5 & 1 & 0 & 0 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right]](/latexrender/pictures/0300efe2f869d7ff98c3bd10e5f5c0e9.png)
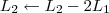
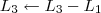
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 2 & -5 & 4 & 0 & 1 & 0 \\ 1 & 2 & 1 & 0 & 0 & 1 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right]](/latexrender/pictures/d56718e58c14e6be4a675798d0b2c218.png)
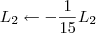
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & -15 & -8 & -2 & 1 & -2 \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right]](/latexrender/pictures/bf92d321716c471edd90a6d9d4a9323d.png)
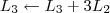
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & -3 & -5 & -1 & 0 & 0 \end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right]](/latexrender/pictures/8bbd6a7495d616b3577aeb425fd217a5.png)
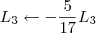
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & -\frac{17}{5} & -\frac{3}{5} & -\frac{1}{5} & \frac{2}{5}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/a18e87a70e18a740ac1a1e48d3e9a375.png)
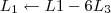
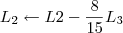
![\left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 6 & 1 & 0 & 1 \\ 0 & 1 & \frac{8}{15} & \frac{2}{15} & -\frac{1}{15} & \frac{2}{15} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/61fdfca5f5d28b7cf66be0a778fedbbb.png)
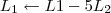
![\left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & -\frac{13}{51} & \frac{7}{51} & \frac{37}{51} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \left[\begin{array}{ccc|ccc} 1 & 5 & 0 & -\frac{1}{17} & -\frac{6}{17} & \frac{29}{17} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right] \sim \left[\begin{array}{ccc|ccc} 1 & 0 & 0 & -\frac{13}{51} & \frac{7}{51} & \frac{37}{51} \\ 0 & 1 & 0 & \frac{2}{51} & -\frac{5}{51} & \frac{10}{51} \\ 0 & 0 & 1 & \frac{3}{17} & \frac{1}{17} & -\frac{2}{17}\end{array}\right]](/latexrender/pictures/95113ef6e8f4c96b29789121f4cc76a3.png)
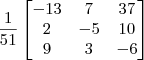
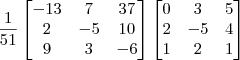
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.