 por Andrewo » Ter Jan 31, 2012 14:10
por Andrewo » Ter Jan 31, 2012 14:10
Aí pessoal, blza?
Alguns problemas de operações de radicais.
Eu sei as propriedades da radiciação mas to boiando, não consegui nem chegar perto de fazer algum desses probleminhas.
1 -
![\left( 3\sqrt[3]{2} \right) . \left( 5\sqrt[3]{6} \right) . \left( 8\sqrt[3]{4} \right) \left( 3\sqrt[3]{2} \right) . \left( 5\sqrt[3]{6} \right) . \left( 8\sqrt[3]{4} \right)](/latexrender/pictures/bbb30bf1d6fb7ffd7f8cdbbadfbdb83f.png)
O que eu tentei fazer : 3.5.6 = 120 2.6.4 = 48 ou seja
![120\sqrt[3]{48} 120\sqrt[3]{48}](/latexrender/pictures/65678eea488425a4aed378a90ca171a2.png)
Mas tá errado, a resposta segundo gabarito é 240
2 -
![\sqrt[]{5} . \sqrt[3]{{5}^{2}} \sqrt[]{5} . \sqrt[3]{{5}^{2}}](/latexrender/pictures/826ae2b039111ccf5dfc1f5b1e69bc2e.png)
Tentei aplicar aquela propriedade p multiplicar raízes de índices diferentes mas não deu certo tbm
Resposta =
![5\sqrt[6]{5} 5\sqrt[6]{5}](/latexrender/pictures/26dd96cc948c6b4d675c7fc1bb7b3e52.png)
3 -
![\frac{\sqrt[4]{5} . \sqrt[3]{6}}{\sqrt[]{15}} \frac{\sqrt[4]{5} . \sqrt[3]{6}}{\sqrt[]{15}}](/latexrender/pictures/ea5397aefe1699053b958b003a94d4d8.png)
Resposta :
![\sqrt[12]{\frac{16}{1125}} \sqrt[12]{\frac{16}{1125}}](/latexrender/pictures/52b5bd8c4033bae3266241b7d68b8ffa.png)
4 -
![\sqrt[]{27} + \sqrt[]{48} - \sqrt[]{12} \sqrt[]{27} + \sqrt[]{48} - \sqrt[]{12}](/latexrender/pictures/d950e3b2a05dd97faed37260b3ec54cc.png)
Resposta
![5\sqrt[]{3} 5\sqrt[]{3}](/latexrender/pictures/6eb158a5108e2c14ec9a8d18c5811a8f.png)
5 -
![5\sqrt[]{2} - 3\sqrt[]{50} + 7\sqrt[]{288} 5\sqrt[]{2} - 3\sqrt[]{50} + 7\sqrt[]{288}](/latexrender/pictures/c37a7fc3003ea49ac77583504e6b9197.png)
Resposta =
![74 \sqrt[]{2} 74 \sqrt[]{2}](/latexrender/pictures/e59e948e4bbc97616c8f5e82c6919544.png)
6 -
![3\sqrt[]{{a}^{3}} - a\sqrt[]{a} + \frac{\sqrt[]{{a}^{5}}}{a} 3\sqrt[]{{a}^{3}} - a\sqrt[]{a} + \frac{\sqrt[]{{a}^{5}}}{a}](/latexrender/pictures/c72d69c6ab8394a1efa9974de8932a6c.png)
Resposta =
![3a\sqrt[]{a} 3a\sqrt[]{a}](/latexrender/pictures/ecdd617d483f342d253dbb6c3908f223.png)
-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Arkanus Darondra » Ter Jan 31, 2012 14:37
por Arkanus Darondra » Ter Jan 31, 2012 14:37
Andrewo escreveu:1 -
![\left( 3\sqrt[3]{2} \right) . \left( 5\sqrt[3]{6} \right) . \left( 8\sqrt[3]{4} \right) \left( 3\sqrt[3]{2} \right) . \left( 5\sqrt[3]{6} \right) . \left( 8\sqrt[3]{4} \right)](/latexrender/pictures/bbb30bf1d6fb7ffd7f8cdbbadfbdb83f.png)
O que eu tentei fazer : 3.5.6 = 120 2.6.4 = 48 ou seja
![120\sqrt[3]{48} 120\sqrt[3]{48}](/latexrender/pictures/65678eea488425a4aed378a90ca171a2.png)
Mas tá errado, a resposta segundo gabarito é 240
Fatore o número 48. Você chegará a resposta
![240\sqrt[3]{6} 240\sqrt[3]{6}](/latexrender/pictures/d25c3cd5cfe44ff27dd5ec210100c8f3.png)
.
Andrewo escreveu:2 -
![\sqrt[]{5} . \sqrt[3]{{5}^{2}} \sqrt[]{5} . \sqrt[3]{{5}^{2}}](/latexrender/pictures/826ae2b039111ccf5dfc1f5b1e69bc2e.png)
Tentei aplicar aquela propriedade p multiplicar raízes de índices diferentes mas não deu certo tbm
Resposta =
![5\sqrt[6]{5} 5\sqrt[6]{5}](/latexrender/pictures/26dd96cc948c6b4d675c7fc1bb7b3e52.png)
![\sqrt{5}.\sqrt[3]{{5}^{2}} \sqrt{5}.\sqrt[3]{{5}^{2}}](/latexrender/pictures/d1f764868deaa7542040f0b5701cb430.png)
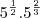
5
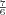
![\sqrt[6]{5^7} \sqrt[6]{5^7}](/latexrender/pictures/47848aa250639e5ea30ea4e211e2811f.png)
![5\sqrt[6]{5} 5\sqrt[6]{5}](/latexrender/pictures/26dd96cc948c6b4d675c7fc1bb7b3e52.png)
Tente fazer os demais. Se não conseguir, volte aqui e mostre o que tentou.

-
Arkanus Darondra
- Colaborador Voluntário

-
- Mensagens: 187
- Registrado em: Seg Dez 26, 2011 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Andrewo » Ter Jan 31, 2012 18:13
por Andrewo » Ter Jan 31, 2012 18:13
A 3 eu realmente não sei, tentei, mas já no desenvolvimento sei que tá errado.
3 -
![\frac{\sqrt[4]{5} . \sqrt[3]{6}}{\sqrt[]{15}} \frac{\sqrt[4]{5} . \sqrt[3]{6}}{\sqrt[]{15}}](/latexrender/pictures/ea5397aefe1699053b958b003a94d4d8.png)
Resposta :
![\sqrt[12]{\frac{16}{1125}} \sqrt[12]{\frac{16}{1125}}](/latexrender/pictures/52b5bd8c4033bae3266241b7d68b8ffa.png)
Nessa daqui eu tentei aplicar a propriedade pra igualar os índices :
![\sqrt[12]{{5}^{3}} . \sqrt[12]{{6}^{4}} = \frac{\sqrt[12]{125} . \sqrt[12]{1296}}{\sqrt[]{15}} \sqrt[12]{{5}^{3}} . \sqrt[12]{{6}^{4}} = \frac{\sqrt[12]{125} . \sqrt[12]{1296}}{\sqrt[]{15}}](/latexrender/pictures/5d5819d71cc99c4a95bdf91f7d83a090.png)
e eu não sei proceder e já imagino que esteja errado e vai dar algum valor absurdo
4 -
![\sqrt[]{27} + \sqrt[]{48} - \sqrt[]{12} \sqrt[]{27} + \sqrt[]{48} - \sqrt[]{12}](/latexrender/pictures/d950e3b2a05dd97faed37260b3ec54cc.png)
Resposta
![5\sqrt[]{3} 5\sqrt[]{3}](/latexrender/pictures/6eb158a5108e2c14ec9a8d18c5811a8f.png)
Essa eu consegui fazer :
![\sqrt[]{{3}^{2}.3} + \sqrt[]{{2}^{2}.{2}^{2}.3} - \sqrt[]{{2}^{2}.3} \sqrt[]{{3}^{2}.3} + \sqrt[]{{2}^{2}.{2}^{2}.3} - \sqrt[]{{2}^{2}.3}](/latexrender/pictures/2cbf57135de6a566da6fb62a1abe1c2f.png)
![\Rightarrow\Rightarrow 3\sqrt[]{3} + 4\sqrt[]{3} - 4\sqrt[]{3} \Rightarrow\Rightarrow 3\sqrt[]{3} + 4\sqrt[]{3} - 4\sqrt[]{3}](/latexrender/pictures/2302b0afb416386b7089aa0db81d65f6.png) a partir daí eu fiz como vi ja num exercício, existe alguma propriedade que deixa o
a partir daí eu fiz como vi ja num exercício, existe alguma propriedade que deixa o ![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) em evidencia?
em evidencia?Continuando :
![\left(3+4-2 \right)\sqrt[]{3} \rightarrow\Rightarrow\rightarrow\Rightarrow 5\sqrt[]{3} \left(3+4-2 \right)\sqrt[]{3} \rightarrow\Rightarrow\rightarrow\Rightarrow 5\sqrt[]{3}](/latexrender/pictures/33a99c8e1c31c441038a35490cf51cd4.png)
5 -
![5\sqrt[]{2} - 3\sqrt[]{50} + 7\sqrt[]{288} 5\sqrt[]{2} - 3\sqrt[]{50} + 7\sqrt[]{288}](/latexrender/pictures/c37a7fc3003ea49ac77583504e6b9197.png)
Resposta =
![74 \sqrt[]{2} 74 \sqrt[]{2}](/latexrender/pictures/e59e948e4bbc97616c8f5e82c6919544.png)
![5\sqrt[]{2} - 15\sqrt[]{2} + 84\sqrt[]{2} 5\sqrt[]{2} - 15\sqrt[]{2} + 84\sqrt[]{2}](/latexrender/pictures/5613ec6f45d607c0c9f3a95d9c9c9b3a.png)
![\left(5-15+84 \right)\sqrt[]{2} \left(5-15+84 \right)\sqrt[]{2}](/latexrender/pictures/9c8b18a2c7032825f4a90141248b55d7.png)
Mesmo problema do 4, eu quero saber pq a raiz quad. de 2 fica em evidencia![\rightarrow\Rightarrow\rightarrow\Rightarrow 74\sqrt[]{2} \rightarrow\Rightarrow\rightarrow\Rightarrow 74\sqrt[]{2}](/latexrender/pictures/fe1da717287de04e4215c5ce5e3830d3.png)
6 -
![3\sqrt[]{{a}^{3}} - a\sqrt[]{a} + \frac{\sqrt[]{{a}^{5}}}{a} 3\sqrt[]{{a}^{3}} - a\sqrt[]{a} + \frac{\sqrt[]{{a}^{5}}}{a}](/latexrender/pictures/c72d69c6ab8394a1efa9974de8932a6c.png)
Resposta =
![3a\sqrt[]{a} 3a\sqrt[]{a}](/latexrender/pictures/ecdd617d483f342d253dbb6c3908f223.png)
Vejam se fiz certo:
![3a\sqrt[]{a} - a\sqrt[]{a} + \frac{\sqrt[]{{a}^{2}.{a}^{2}.a}}{a} 3a\sqrt[]{a} - a\sqrt[]{a} + \frac{\sqrt[]{{a}^{2}.{a}^{2}.a}}{a}](/latexrender/pictures/c2dee78839713d4f198ed1a3edcc9a90.png)
=
![3a\sqrt[]{a} - a\sqrt[]{a} + \frac{{a}^{2} \sqrt[]{a}}{a} 3a\sqrt[]{a} - a\sqrt[]{a} + \frac{{a}^{2} \sqrt[]{a}}{a}](/latexrender/pictures/e52290fc0b25d5ed9c27e7e4790e1544.png)
=
![3a\sqrt[]{a} - a\sqrt[]{a} + \sqrt[a]{a} 3a\sqrt[]{a} - a\sqrt[]{a} + \sqrt[a]{a}](/latexrender/pictures/e18b8e25b5c3aebeddc9867fe9849d08.png)
=
![3a\sqrt[]{a} 3a\sqrt[]{a}](/latexrender/pictures/ecdd617d483f342d253dbb6c3908f223.png)
-

Andrewo
- Usuário Parceiro

-
- Mensagens: 54
- Registrado em: Qui Jan 12, 2012 11:22
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Ter Jan 31, 2012 18:38
por LuizAquino » Ter Jan 31, 2012 18:38
Andrewo escreveu:3 -
![\frac{\sqrt[4]{5} . \sqrt[3]{6}}{\sqrt[]{15}} \frac{\sqrt[4]{5} . \sqrt[3]{6}}{\sqrt[]{15}}](/latexrender/pictures/ea5397aefe1699053b958b003a94d4d8.png)
Nessa daqui eu tentei aplicar a propriedade pra igualar os índices :
![\sqrt[12]{{5}^{3}} . \sqrt[12]{{6}^{4}} = \frac{\sqrt[12]{125} . \sqrt[12]{1296}}{\sqrt[]{15}} \sqrt[12]{{5}^{3}} . \sqrt[12]{{6}^{4}} = \frac{\sqrt[12]{125} . \sqrt[12]{1296}}{\sqrt[]{15}}](/latexrender/pictures/87dbbf5c0f245e5421946726887abe7e.png)
e eu não sei proceder e já imagino que esteja errado e vai dar algum valor absurdo
Faça o seguinte:
![\frac{\sqrt[4]{5} \cdot \sqrt[3]{6}}{\sqrt{15}} = \frac{\sqrt[12]{5^3} \cdot \sqrt[12]{6^4}}{\sqrt[12]{15^6}} \frac{\sqrt[4]{5} \cdot \sqrt[3]{6}}{\sqrt{15}} = \frac{\sqrt[12]{5^3} \cdot \sqrt[12]{6^4}}{\sqrt[12]{15^6}}](/latexrender/pictures/708b38dacdff99c77f1a1dbc47d0835b.png)
![= \frac{\sqrt[12]{5^3} \cdot \sqrt[12]{2^4 \cdot 3^4}}{\sqrt[12]{3^6 \cdot 5^6}} = \frac{\sqrt[12]{5^3} \cdot \sqrt[12]{2^4 \cdot 3^4}}{\sqrt[12]{3^6 \cdot 5^6}}](/latexrender/pictures/f84ce0392f7095755f6c9120effc8a5a.png)
![= \sqrt[12]{\frac{5^3 \cdot 2^4 \cdot 3^4}{3^6 \cdot 5^6}} = \sqrt[12]{\frac{5^3 \cdot 2^4 \cdot 3^4}{3^6 \cdot 5^6}}](/latexrender/pictures/357eda601cb169702e2cea046935c8ee.png)
Agora termine a partir daí.
Andrewo escreveu:Essa eu consegui fazer :

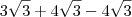
a partir daí eu fiz como vi ja num exercício, existe alguma propriedade que deixa o

em evidencia?
Continuando :
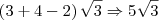
Imagine que você deseja somar 3x com 5x. Você pode representar isso por 3x + 5x. Como você já sabe, isso é igual a 8x.
Uma outra forma de enxergar essa operação é colocando o x em envidência. Você terá que: 3x + 5x = (3 + 5)x = 8x.
Agora imagine que você deseja somar

com
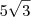
. Qual será o resultado? Basta usar a mesma ideia exibida no exemplo anterior. O resultado será
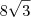
. Nesse caso, o termo

está fazendo o mesmo papel do x no exemplo anterior.
No último passo, há um erro de digitação. Ao invés de
![\sqrt[a]{a} \sqrt[a]{a}](/latexrender/pictures/6739b136dfb6969a12d9d8520d038d6d.png)
o correto é
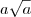
. O resto está ok.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por LuizAquino » Qua Fev 01, 2012 13:53
por LuizAquino » Qua Fev 01, 2012 13:53
Andrewo escreveu:Eu tenho que usar a propriedade pra igualar os índices tanto pro numerador quanto pro denominador?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Operaçoes com Radicais] AJUDA.!bom
por RenanRodrigues » Sex Out 07, 2011 11:32
- 1 Respostas
- 1210 Exibições
- Última mensagem por Neperiano

Dom Out 09, 2011 15:00
Números Complexos
-
- Operações com radicais, potência de expoente fracionário...
por brunofelixinho » Ter Nov 12, 2013 20:45
- 0 Respostas
- 1768 Exibições
- Última mensagem por brunofelixinho

Ter Nov 12, 2013 20:45
Álgebra Elementar
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2336 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
-
- Radicais
por Andrewo » Qua Fev 01, 2012 13:43
- 8 Respostas
- 4127 Exibições
- Última mensagem por LuizAquino

Qua Fev 08, 2012 12:22
Álgebra Elementar
-
- Radicais II
por Andrewo » Qui Fev 09, 2012 19:38
- 3 Respostas
- 1877 Exibições
- Última mensagem por MarceloFantini

Sex Fev 10, 2012 11:32
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\left( 3\sqrt[3]{2} \right) . \left( 5\sqrt[3]{6} \right) . \left( 8\sqrt[3]{4} \right) \left( 3\sqrt[3]{2} \right) . \left( 5\sqrt[3]{6} \right) . \left( 8\sqrt[3]{4} \right)](/latexrender/pictures/bbb30bf1d6fb7ffd7f8cdbbadfbdb83f.png)
![120\sqrt[3]{48} 120\sqrt[3]{48}](/latexrender/pictures/65678eea488425a4aed378a90ca171a2.png)
![\sqrt[]{5} . \sqrt[3]{{5}^{2}} \sqrt[]{5} . \sqrt[3]{{5}^{2}}](/latexrender/pictures/826ae2b039111ccf5dfc1f5b1e69bc2e.png) Tentei aplicar aquela propriedade p multiplicar raízes de índices diferentes mas não deu certo tbm
Tentei aplicar aquela propriedade p multiplicar raízes de índices diferentes mas não deu certo tbm![5\sqrt[6]{5} 5\sqrt[6]{5}](/latexrender/pictures/26dd96cc948c6b4d675c7fc1bb7b3e52.png)
![\frac{\sqrt[4]{5} . \sqrt[3]{6}}{\sqrt[]{15}} \frac{\sqrt[4]{5} . \sqrt[3]{6}}{\sqrt[]{15}}](/latexrender/pictures/ea5397aefe1699053b958b003a94d4d8.png)
![\sqrt[12]{\frac{16}{1125}} \sqrt[12]{\frac{16}{1125}}](/latexrender/pictures/52b5bd8c4033bae3266241b7d68b8ffa.png)
![\sqrt[]{27} + \sqrt[]{48} - \sqrt[]{12} \sqrt[]{27} + \sqrt[]{48} - \sqrt[]{12}](/latexrender/pictures/d950e3b2a05dd97faed37260b3ec54cc.png)
![5\sqrt[]{3} 5\sqrt[]{3}](/latexrender/pictures/6eb158a5108e2c14ec9a8d18c5811a8f.png)
![5\sqrt[]{2} - 3\sqrt[]{50} + 7\sqrt[]{288} 5\sqrt[]{2} - 3\sqrt[]{50} + 7\sqrt[]{288}](/latexrender/pictures/c37a7fc3003ea49ac77583504e6b9197.png)
![74 \sqrt[]{2} 74 \sqrt[]{2}](/latexrender/pictures/e59e948e4bbc97616c8f5e82c6919544.png)
![3\sqrt[]{{a}^{3}} - a\sqrt[]{a} + \frac{\sqrt[]{{a}^{5}}}{a} 3\sqrt[]{{a}^{3}} - a\sqrt[]{a} + \frac{\sqrt[]{{a}^{5}}}{a}](/latexrender/pictures/c72d69c6ab8394a1efa9974de8932a6c.png)
![3a\sqrt[]{a} 3a\sqrt[]{a}](/latexrender/pictures/ecdd617d483f342d253dbb6c3908f223.png)


![240\sqrt[3]{6} 240\sqrt[3]{6}](/latexrender/pictures/d25c3cd5cfe44ff27dd5ec210100c8f3.png) .
.![\sqrt{5}.\sqrt[3]{{5}^{2}} \sqrt{5}.\sqrt[3]{{5}^{2}}](/latexrender/pictures/d1f764868deaa7542040f0b5701cb430.png)
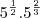
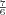
![\sqrt[6]{5^7} \sqrt[6]{5^7}](/latexrender/pictures/47848aa250639e5ea30ea4e211e2811f.png)


![\sqrt[12]{{5}^{3}} . \sqrt[12]{{6}^{4}} = \frac{\sqrt[12]{125} . \sqrt[12]{1296}}{\sqrt[]{15}} \sqrt[12]{{5}^{3}} . \sqrt[12]{{6}^{4}} = \frac{\sqrt[12]{125} . \sqrt[12]{1296}}{\sqrt[]{15}}](/latexrender/pictures/5d5819d71cc99c4a95bdf91f7d83a090.png) e eu não sei proceder e já imagino que esteja errado e vai dar algum valor absurdo
e eu não sei proceder e já imagino que esteja errado e vai dar algum valor absurdo![\sqrt[]{{3}^{2}.3} + \sqrt[]{{2}^{2}.{2}^{2}.3} - \sqrt[]{{2}^{2}.3} \sqrt[]{{3}^{2}.3} + \sqrt[]{{2}^{2}.{2}^{2}.3} - \sqrt[]{{2}^{2}.3}](/latexrender/pictures/2cbf57135de6a566da6fb62a1abe1c2f.png)
![\Rightarrow\Rightarrow 3\sqrt[]{3} + 4\sqrt[]{3} - 4\sqrt[]{3} \Rightarrow\Rightarrow 3\sqrt[]{3} + 4\sqrt[]{3} - 4\sqrt[]{3}](/latexrender/pictures/2302b0afb416386b7089aa0db81d65f6.png)
![\sqrt[]{3} \sqrt[]{3}](/latexrender/pictures/b84ccc0f808c82dca2d7b0f887c64445.png) em evidencia?
em evidencia?![\left(3+4-2 \right)\sqrt[]{3} \rightarrow\Rightarrow\rightarrow\Rightarrow 5\sqrt[]{3} \left(3+4-2 \right)\sqrt[]{3} \rightarrow\Rightarrow\rightarrow\Rightarrow 5\sqrt[]{3}](/latexrender/pictures/33a99c8e1c31c441038a35490cf51cd4.png)
![5\sqrt[]{2} - 15\sqrt[]{2} + 84\sqrt[]{2} 5\sqrt[]{2} - 15\sqrt[]{2} + 84\sqrt[]{2}](/latexrender/pictures/5613ec6f45d607c0c9f3a95d9c9c9b3a.png)
![\left(5-15+84 \right)\sqrt[]{2} \left(5-15+84 \right)\sqrt[]{2}](/latexrender/pictures/9c8b18a2c7032825f4a90141248b55d7.png)
![\rightarrow\Rightarrow\rightarrow\Rightarrow 74\sqrt[]{2} \rightarrow\Rightarrow\rightarrow\Rightarrow 74\sqrt[]{2}](/latexrender/pictures/fe1da717287de04e4215c5ce5e3830d3.png)
![3a\sqrt[]{a} - a\sqrt[]{a} + \frac{\sqrt[]{{a}^{2}.{a}^{2}.a}}{a} 3a\sqrt[]{a} - a\sqrt[]{a} + \frac{\sqrt[]{{a}^{2}.{a}^{2}.a}}{a}](/latexrender/pictures/c2dee78839713d4f198ed1a3edcc9a90.png)
![3a\sqrt[]{a} - a\sqrt[]{a} + \frac{{a}^{2} \sqrt[]{a}}{a} 3a\sqrt[]{a} - a\sqrt[]{a} + \frac{{a}^{2} \sqrt[]{a}}{a}](/latexrender/pictures/e52290fc0b25d5ed9c27e7e4790e1544.png)
![3a\sqrt[]{a} - a\sqrt[]{a} + \sqrt[a]{a} 3a\sqrt[]{a} - a\sqrt[]{a} + \sqrt[a]{a}](/latexrender/pictures/e18b8e25b5c3aebeddc9867fe9849d08.png)
![\sqrt[12]{{5}^{3}} . \sqrt[12]{{6}^{4}} = \frac{\sqrt[12]{125} . \sqrt[12]{1296}}{\sqrt[]{15}} \sqrt[12]{{5}^{3}} . \sqrt[12]{{6}^{4}} = \frac{\sqrt[12]{125} . \sqrt[12]{1296}}{\sqrt[]{15}}](/latexrender/pictures/87dbbf5c0f245e5421946726887abe7e.png) e eu não sei proceder e já imagino que esteja errado e vai dar algum valor absurdo
e eu não sei proceder e já imagino que esteja errado e vai dar algum valor absurdo![\frac{\sqrt[4]{5} \cdot \sqrt[3]{6}}{\sqrt{15}} = \frac{\sqrt[12]{5^3} \cdot \sqrt[12]{6^4}}{\sqrt[12]{15^6}} \frac{\sqrt[4]{5} \cdot \sqrt[3]{6}}{\sqrt{15}} = \frac{\sqrt[12]{5^3} \cdot \sqrt[12]{6^4}}{\sqrt[12]{15^6}}](/latexrender/pictures/708b38dacdff99c77f1a1dbc47d0835b.png)
![= \frac{\sqrt[12]{5^3} \cdot \sqrt[12]{2^4 \cdot 3^4}}{\sqrt[12]{3^6 \cdot 5^6}} = \frac{\sqrt[12]{5^3} \cdot \sqrt[12]{2^4 \cdot 3^4}}{\sqrt[12]{3^6 \cdot 5^6}}](/latexrender/pictures/f84ce0392f7095755f6c9120effc8a5a.png)
![= \sqrt[12]{\frac{5^3 \cdot 2^4 \cdot 3^4}{3^6 \cdot 5^6}} = \sqrt[12]{\frac{5^3 \cdot 2^4 \cdot 3^4}{3^6 \cdot 5^6}}](/latexrender/pictures/357eda601cb169702e2cea046935c8ee.png)

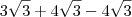 a partir daí eu fiz como vi ja num exercício, existe alguma propriedade que deixa o
a partir daí eu fiz como vi ja num exercício, existe alguma propriedade que deixa o  em evidencia?
em evidencia?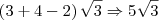
 com
com 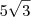 . Qual será o resultado? Basta usar a mesma ideia exibida no exemplo anterior. O resultado será
. Qual será o resultado? Basta usar a mesma ideia exibida no exemplo anterior. O resultado será 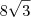 . Nesse caso, o termo
. Nesse caso, o termo 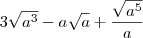
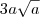
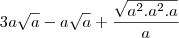
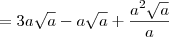
![=3a\sqrt{a} - a\sqrt{a} + \sqrt[a]{a} =3a\sqrt{a} - a\sqrt{a} + \sqrt[a]{a}](/latexrender/pictures/bfd0689a84ff6ba1798ce21d4c9cef64.png)
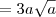
![\sqrt[a]{a} \sqrt[a]{a}](/latexrender/pictures/6739b136dfb6969a12d9d8520d038d6d.png) o correto é
o correto é 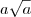 . O resto está ok.
. O resto está ok.
![\sqrt[12]{\frac{{2}^{4}}{{3}^{2}.{5}^{3}}} \sqrt[12]{\frac{{2}^{4}}{{3}^{2}.{5}^{3}}}](/latexrender/pictures/0ba3cf10ed5b93382f637882511c0a5e.png)