Quando nasceu seu filho, Armando abriu uma poupança e depositou R$20,00. Armando fez novos depósitos a cada aniversário do filho, aumentando sempre o valor em R$5,00, de um dépósito para outro. Após o depósito referente ao 25º aniversário de seu filho, quanto Armando terá depositado desde o nascimento de seu filho?
Minha tentativa:
Sendo uma PA, temos:
r=5
a1=20
Calculei na fórmula a25= 140,00
Depois pela fórmula da soma dos termos de uma PA:
Sn=2000,00 ( dois mil reais )
No gabarito tem q dar 2.145,00. Eu errei ou o gabarito está errado. Desde já agradeço muitissimo!!!!


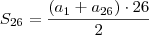



 , avisa que eu resolvo.
, avisa que eu resolvo.

