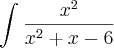
Sabendo que:
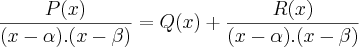
Tenho que:
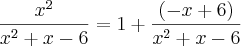
Então:
![\int_{}^{}\left[ 1+\frac{\left(-x+6 \right)}{{x}^{2}+x-6}\right]dx = \int_{}^{}1 dx+\int_{}^{}\frac{(-x+6)}{{x}^{2}+x-6}dx \int_{}^{}\left[ 1+\frac{\left(-x+6 \right)}{{x}^{2}+x-6}\right]dx = \int_{}^{}1 dx+\int_{}^{}\frac{(-x+6)}{{x}^{2}+x-6}dx](/latexrender/pictures/4ab67acf64b5dea9213f4a72efe335d2.png)
Fazendo A e B:
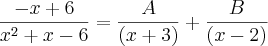

Fazendo x=2, obtemos B = 4/5 e com x=-3 obtemos A=-9/5
Fazendo as integrais:
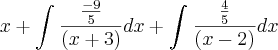
Temos então:
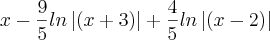
(Depois posto as outras resoluções)
Grato

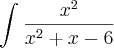
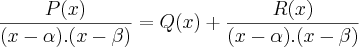
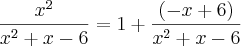
![\int_{}^{}\left[ 1+\frac{\left(-x+6 \right)}{{x}^{2}+x-6}\right]dx = \int_{}^{}1 dx+\int_{}^{}\frac{(-x+6)}{{x}^{2}+x-6}dx \int_{}^{}\left[ 1+\frac{\left(-x+6 \right)}{{x}^{2}+x-6}\right]dx = \int_{}^{}1 dx+\int_{}^{}\frac{(-x+6)}{{x}^{2}+x-6}dx](/latexrender/pictures/4ab67acf64b5dea9213f4a72efe335d2.png)
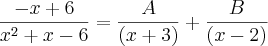

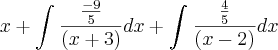
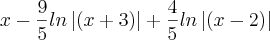

integrate (x^2)/(x^2+x-6) dx


valeuleo escreveu:Esse site resolve de uma maneira "não acadêmica rsrs". O meu deu diferente, mas os procedimentos da página são outros.
For the integrand, do long division:
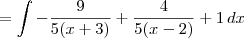
is the natural logarithm
 representa
representa 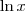 , a solução apresentada é a mesma que a sua!
, a solução apresentada é a mesma que a sua!

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes

 .
.
 :
: