Brother eu fiz ate aqui mas travei me ajuda aew por favor...

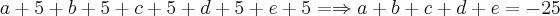


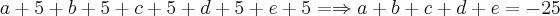

Numa família há 5 pessoas sucedendo-se com 5 anos de intervalo.
Raphael Feitas10 escreveu:Calcular a soma das suas idades, sabendo-se que o primogênito tem o dobro da idade do mais novo.

 que fica no caso
que fica no caso  que jogando n que é 10 nas idades de cada pessoa vai achar 15,20,25,30 que somando essas idades todas dá 100. e jogando n que é 10 nessa outra equação
que jogando n que é 10 nas idades de cada pessoa vai achar 15,20,25,30 que somando essas idades todas dá 100. e jogando n que é 10 nessa outra equação 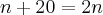 acha
acha  aew soma no caso
aew soma no caso  acha a resposta mas deve ta errado né brother pq 30 ñ é o dobro de 20 me corrija aew por favor...
acha a resposta mas deve ta errado né brother pq 30 ñ é o dobro de 20 me corrija aew por favor...
Raphael Feitas10 escreveu:Brother eu somei as idades e achei


Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: