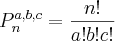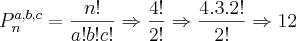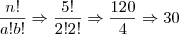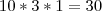estou tendo dificuldade em calcular as possibilidade de forma uma centena de acordo um conjuto de elementos
exemplo:
elementos 1,2,3,4
tentei assim
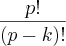
sendo p= numero de elementos = 4
k = 3
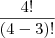 = 24
= 24ate ai funcionou mais agora não da certo com os elementos 1,1,2,3 ou seja quando teve a repetição de um elemento ( 1 )
sei q o resultado teria q ser 12 gostaria de saber o caminho para se chegar a esse resultado sendo q tenho q fazer uma forma q ele aceite aumentar o numero de elementos e tbm de repetições
obrigado