GRAU MINUTO E SEGUNDO

por **Lauraaaaaa** » Dom Jul 31, 2011 14:38

Com as ferias , eu esqueci t-u-d-o

E eu tenho que fazer essa lista de exercicios , e nao to conseguindo fazer os de grau minuto e segundo . Faltei na aula em que ele explicou essa materia , e mesmo eu copiando , nao achei nada que me ajudasse .

São dois :
Se 3/4 de um angulo é igual a 103º35'12'', qual é a medida desse angulo ?
DETERMINE 8/5 de 27º39'45''

Bom , esses me deram duvidas .
Eu tenho a resposta : a do primeiro é 1388º06'56''
e a do sugundo é 44º15'36''
Obrigada mesmo

por **Molina** » Dom Jul 31, 2011 15:52

Boa tarde.

O primeiro você tem uma equação do tipo:

$\frac{3}{4}x=103\º35'12'' \Rightarrow x = \frac{4*103\º35'12''}{3}$

onde x é o ângulo que você quer descobrir.

A segunda questão você quer saber quanto vale:

$\frac{8}{5}*27\º39'45''$

Vou fazer esta e o procedimento é análogo para a primeira:

$\frac{8}{5}*27\º39'45'' = \frac{216\º312'360''}{5} = \frac{216\º318'0''}{5} = \frac{221\º18'0''}{5}$

Fazendo a divisão separadamente dos termos, começando pelo grau, temos:

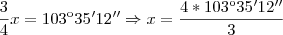
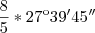
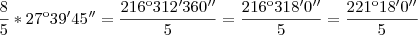
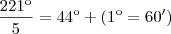$\frac{221\º}{5}= 44\º + (1\º=60')$ este 60' que "sobrou" desta divisão vamos adicionar na conta abaixo:

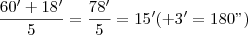$\frac{60'+18'}{5}=\frac{78'}{5}= 15' (+3'=180")$ este 180'' que "sobrou" desta divisão vamos adicionar na conta abaixo: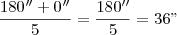

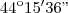
$\frac{180''+0''}{5}=\frac{180''}{5}=36"$

Juntando todos os termos, obtemos:

$44\º15'36"$

Qualquer dúvida, informe! :y:

GRAU MINUTO E SEGUNDO

GRAU MINUTO E SEGUNDO

GRAU MINUTO E SEGUNDO

Re: GRAU MINUTO E SEGUNDO

Quem está online