Volume do Cone

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Volume do Cone

Regras do fórum
Responder

Volume do Cone

Mensagempor garciarafael » Seg Jul 18, 2011 22:00

Questão:
Um cone circular reto tem em seu interior 400ml de certo líquido, ocupando 2/5 de sua altura. A capacidade desse cone, em litros, é?

Alguém pode me ajudar?

Abraços
garciarafael
Novo Usuário
Novo Usuário
 
Mensagens: 3
Registrado em: Seg Jul 18, 2011 21:50
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo

Re: Volume do Cone

Mensagempor garciarafael » Seg Jul 18, 2011 23:26

Ngm? =/...

O gabarito dis que a resposta é 6,25L.

Alguém sabe resolver?
garciarafael
Novo Usuário
Novo Usuário
 
Mensagens: 3
Registrado em: Seg Jul 18, 2011 21:50
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo

Re: Volume do Cone

Mensagempor FilipeCaceres » Seg Jul 18, 2011 23:47

Olá garciarafael,

Para resolver está questão basta você ter conhecimentos da relação volume e altura, dado por:
\frac{v_1}{v_2}=\left(\frac{h_1}{h_2}\right)^3

Do enunciado temos:
v_1=400\,ml
h_1=\frac{2}{5}h_2

Logo,
\frac{400}{v_2}=\left(\frac{2h_2}{5h_2}\right)^3=\frac{8}{125}

v_2=6250\,ml

\boxed{v_2=6,25\,l}

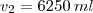
Abraço.
FilipeCaceres
Colaborador Voluntário
Colaborador Voluntário
 
Mensagens: 351
Registrado em: Dom Out 31, 2010 21:43
Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
Área/Curso: Tec. Mecatrônica
Andamento: formado
Voltar ao topo

Re: Volume do Cone

Mensagempor garciarafael » Seg Jul 18, 2011 23:52

É cara, bacana.

No meu livro nao tem essa fórmula sabe. E voltei a estudar hoje praticamente, dps de 2 anos parado, ai ta meio difícil de entender nesse início...

Mas valeu, brigadão
garciarafael
Novo Usuário
Novo Usuário
 
Mensagens: 3
Registrado em: Seg Jul 18, 2011 21:50
Formação Escolar: ENSINO MÉDIO
Andamento: cursando
Voltar ao topo
Responder

Voltar para Geometria Espacial

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 


Tópico Popular

Assunto: simplifiquei e achei...está certo?????????????
Autor: zig - Sex Set 23, 2011 13:57

{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}

Assunto: simplifiquei e achei...está certo?????????????
Autor: Vennom - Sex Set 23, 2011 21:41

zig escreveu:{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}


Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo: {\frac{1}{4}}^{-1} = \frac{4}{1}

Então pense o seguinte: a fração geratriz de 0,05 é \frac{1}{20} , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja: {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}

A raiz quadrada de vinte, você acha fácil, né?

Espero ter ajudado.

Assunto: simplifiquei e achei...está certo?????????????
Autor: fraol - Dom Dez 11, 2011 20:23

Nós podemos simplificar, um pouco, sqrt(20) da seguinte forma:

sqrt(20) = sqrt(4 . 5) = sqrt( 2^2 . 5 ) = 2 sqrt(5).

É isso.

Assunto: simplifiquei e achei...está certo?????????????
Autor: fraol - Dom Dez 11, 2011 20:24

Nós podemos simplificar, um pouco, \sqrt(20) da seguinte forma:

\sqrt(20) = \sqrt(4 . 5) = \sqrt( 2^2 . 5 ) = 2 \sqrt(5).

É isso.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

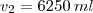
Índice do fórum