
Eu não estou conseguindo resolver uma integral, ae procurei por exemplos pela internet, mas não consegui nada, foi ae que encontrei esse site e decidi postar aki para ver se alguém me ajuda ^^
Caso alguém possa me ajudar é o seguinte:
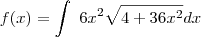
Eu não lembro mais como se resolve esse tipo de integral , eu estava tentando fazer uma substituição de variavél x para u de modo que a ficasse com uma cara mais simples:
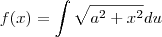
e assim resolver por substituição trogonométrica, mas não consegui fazer a simplificação.


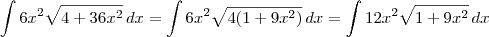
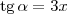 .
.

 .
.
 :
: