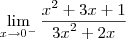
Em evidência, achei:
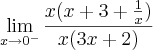
Daí não consigo mais.
Fiz vários cálculos, mas não consegui chegar em um resultado seguro.
Algúem aí?
Obrigado.

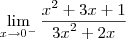
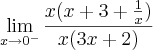


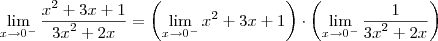

 =
= 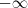 ?
?
Fabio Cabral escreveu:Simples assim?
Com resultado:?


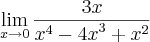
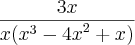
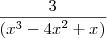
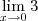 .
. 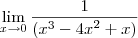

A pergunta é: O resultado é realmente 0 ? Isto esta correto?
É verdade que só posso usar evidenciar quando x tende a 0, - infinito e + infinito?

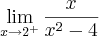
 . Correto?
. Correto?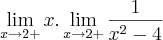
 =
= 

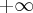

Fabio Cabral escreveu:Compreendi.
Levando em conta esse limite :
Não posso usar evidência por não ser 0, nem. Correto?
Então, fiz da seguinte forma:
Agora sim, ficaria 2 .=
Estou correto? Posso fazer dessa forma?



Claudin escreveu:"Logo, isso gerará o seguinte cálculo:
3 . 0 = 0
A pergunta é: O resultado é realmente 0 ? Isto esta correto?"
O resultado do segundo limite seria
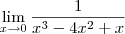 não existe, pois os laterais são distintos. Ou seja, temos que:
não existe, pois os laterais são distintos. Ou seja, temos que: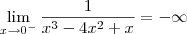
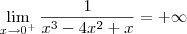
Fabio Cabral escreveu:
Agora sim, ficaria
Estou correto? Posso fazer dessa forma?



Fabio Cabral escreveu:
Agora sim, ficaria
Estou correto? Posso fazer dessa forma?
 fosse a mesma coisa que
fosse a mesma coisa que 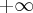 .
.


Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)