Se os lados de um triângulo medem x, x+1 e x+2, então, para qualquer x real e maior que 1, o cosseno do maior ângulo interno desse triângulo é igual a:
Eu fiz assim...
O maior ângulo interno é o que se opõe ao maior lado, logo, ângulo oposto a x+2.
Sendo assim, pela lei dos cossenos, sendo alpha o maior ângulo interno deste triângulo...
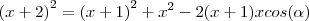
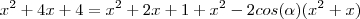
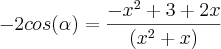
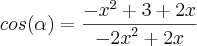
No meu livro a resposta é
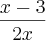 ...
...Agradeço desde já!



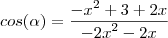
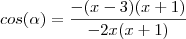
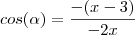
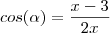




 .
.
 :
: