1-) Determine a soma dos coeficientes do desenvolvimento de
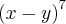 .
.Não sei nem como começar! =/
2-) (Ufop-MG) No desenvolvimento de
![\left({x + \frac{1}{\sqrt[3]{x}}} \right)^{6} \left({x + \frac{1}{\sqrt[3]{x}}} \right)^{6}](/latexrender/pictures/f787edeb7d61941cd3613c997260445d.png) , calcule a ordem e o coeficiente do termo em x².
, calcule a ordem e o coeficiente do termo em x².Estou me confundindo (creio eu) com justamente o desafio dessa questão, que é a raiz cúbica no denominador.
3-) No desenvolvimento do binômio
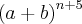 , ordenado segundo as potências decrescentes de a, o quociente do (n + 3)-ésimo termo pelo (n + 1)-ésimo termo é
, ordenado segundo as potências decrescentes de a, o quociente do (n + 3)-ésimo termo pelo (n + 1)-ésimo termo é 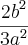 , isto é,
, isto é, 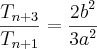 . Determine n.
. Determine n.Desde já agradeço!
Giles.



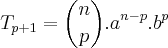 , onde
, onde 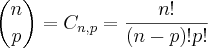
 é o 5° termo, ou seja, p = 4.
é o 5° termo, ou seja, p = 4.

 .
.
 :
: