 por Giles » Qua Nov 05, 2008 19:31
por Giles » Qua Nov 05, 2008 19:31
Olá, gostaria que alguém me ajuda-se nesses exercícios de Binômio que não consegui:
1-) Determine a soma dos coeficientes do desenvolvimento de
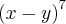
.
Não sei nem como começar! =/2-) (Ufop-MG) No desenvolvimento de
![\left({x + \frac{1}{\sqrt[3]{x}}} \right)^{6} \left({x + \frac{1}{\sqrt[3]{x}}} \right)^{6}](/latexrender/pictures/f787edeb7d61941cd3613c997260445d.png)
, calcule a ordem e o coeficiente do termo em
x².
Estou me confundindo (creio eu) com justamente o desafio dessa questão, que é a raiz cúbica no denominador.3-) No desenvolvimento do binômio
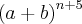
, ordenado segundo as potências decrescentes de
a, o quociente do (n + 3)-ésimo termo pelo (n + 1)-ésimo termo é
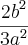
, isto é,
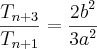
. Determine
n.
Desde já agradeço!
Giles.
"As pessoas que vencem nessa vida são aquelas que procuram as circunstâncias de que precisam e quando não as encontram, as criam"
-

Giles
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Dom Out 19, 2008 11:14
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Construção Civil Integr
- Andamento: cursando
 por Molina » Qui Nov 06, 2008 00:23
por Molina » Qui Nov 06, 2008 00:23
Giles escreveu:Olá, gostaria que alguém me ajuda-se nesses exercícios de Binômio que não consegui:
1-) Determine a soma dos coeficientes do desenvolvimento de
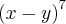
.
Olá Giles,
A soma dos coeficientes de
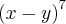
, basta pegar os coeficientes de x e de y, somá-los e elevar o resultado a potência do binômio, neste caso, a potência é 7.
O resultado obtido é a soma dos coeficientes.
Bom estudo!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Qui Nov 06, 2008 00:40
por Molina » Qui Nov 06, 2008 00:40
Giles escreveu:Olá, gostaria que alguém me ajuda-se nesses exercícios de Binômio que não consegui:
2-) (Ufop-MG) No desenvolvimento de
![\left({x + \frac{1}{\sqrt[3]{x}}} \right)^{6} \left({x + \frac{1}{\sqrt[3]{x}}} \right)^{6}](/latexrender/pictures/f787edeb7d61941cd3613c997260445d.png)
, calcule a ordem e o coeficiente do termo em
x².
Você precisa utilizar a
Fórmula do termo geral de um Binômio de Newton:
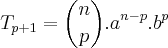
, onde
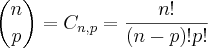
No caso de um polinômio de grau 6, o termo

é o 5° termo, ou seja, p = 4.
Tente resolver a partir daí.
Caso não consigo coloque suas dúvidas e onde parou aqui no fórum que alguem irá lhe auxiliar.
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- não consigo resolver estas questões
por igorluanabianca » Sex Jul 24, 2009 19:58
- 2 Respostas
- 3799 Exibições
- Última mensagem por Cleyson007

Sáb Jul 25, 2009 09:52
Matemática Financeira
-
- nao consigo resolver essas questoes
por janair sousa » Ter Ago 16, 2011 16:17
- 4 Respostas
- 2528 Exibições
- Última mensagem por janair sousa

Sáb Ago 20, 2011 16:27
Logaritmos
-
- não consigo responder as questões de juros simles
por Fran » Seg Ago 10, 2009 14:37
- 2 Respostas
- 3918 Exibições
- Última mensagem por Fran

Qua Ago 12, 2009 13:38
Matemática Financeira
-
- * Trigonometria : Questões simples que não consigo fazer!!!
por Thiago Valenca » Seg Abr 16, 2012 17:38
- 4 Respostas
- 2984 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 21, 2012 17:47
Trigonometria
-
- P.A nao consigo resolver essa p.a.
por Dalila » Sex Nov 14, 2008 16:58
- 2 Respostas
- 3139 Exibições
- Última mensagem por admin

Sex Nov 14, 2008 17:29
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
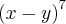 .
.![\left({x + \frac{1}{\sqrt[3]{x}}} \right)^{6} \left({x + \frac{1}{\sqrt[3]{x}}} \right)^{6}](/latexrender/pictures/f787edeb7d61941cd3613c997260445d.png) , calcule a ordem e o coeficiente do termo em x².
, calcule a ordem e o coeficiente do termo em x².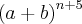 , ordenado segundo as potências decrescentes de a, o quociente do (n + 3)-ésimo termo pelo (n + 1)-ésimo termo é
, ordenado segundo as potências decrescentes de a, o quociente do (n + 3)-ésimo termo pelo (n + 1)-ésimo termo é 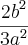 , isto é,
, isto é, 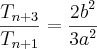 . Determine n.
. Determine n.


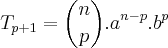 , onde
, onde 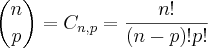
 é o 5° termo, ou seja, p = 4.
é o 5° termo, ou seja, p = 4.
