01. Uma torre de comunicações conta com 5 bandeiras sinalizadoras, e as mensagens são enviadas quando uma ou mais bandeiras são hasteadas. Quantas mensagens distintas podem ser enviadas?
a) 125
b) 245
c) 325
d) 420
e) 640
A priori não tenho uma base para início.
02. A mala do professor Niltinho tem um cadeado cujo segredo é uma combinação com 5 algarismos, cada um dos quais podendo varias de 0 a 9. Ele esqueceu a combinação que escolhera como segredo, mas sabe que atende às seguintes comdições:
I) Se o primeiro algarismo é ímpar, então o último algarismo também é ímpar;
II) Se o primeiro algarismo é par, então o último algarismo é igual ao primeiro;
III) A soma do segundo e terceiro algarismos é igual a 5.
Quantas combinações diferentes atendem às condições estabelecidas pelo professor Niltrinho?
a) 1.175
b) 1.320
c) 1.640
d) 1.800
e) 1.940
Tentei resolvê-la assim;
Considerando o inciso I: 5._._.5 (sendo os travessões completados pelas combinações: 0 e 5; 1 e 4; 2 e 3; 3 e 2; 4 e 1; 5 e 0, respectivamente). Em síntese será o produto de 6 (combinações para a soma ser 5) e 25 (inciso I). Já com o inciso III tem-se: 5._._.1, utilizando as mesmas combinações já citadas o resultado é o produto de 5 (inciso III) e 6 (combinações). Somando 150 e 30 obtém-se 180, não correspondendo nenhuma alternativa com isto.
Por favor ajudem-me, desde já obrigado.

 mensagens.
mensagens.
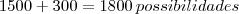
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.