Tenho bastante dificuldade de trabalhar com divisões com variaveis com potência. Gostaria de saber como posso solucionar a quastão abaixo e se existe algum tipo de regra geral, quando o divisor é = 1.
Dado o polinômio A(x) =
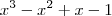 , obtemos o quociente
, obtemos o quociente  e o resto
e o resto  quando dividido pelo polinômio B(x). Para
quando dividido pelo polinômio B(x). Para 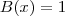 ,
,  será igual a?
será igual a?Desde já, agradeço atenção, estou precisando bastante desta resposta.]
Bjos.


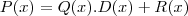
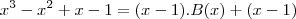
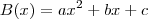 ,ou seja, deve ser do 2º grau.
,ou seja, deve ser do 2º grau. 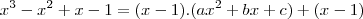
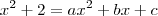




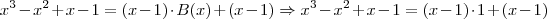
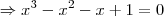
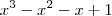 por
por  , o que resulta em
, o que resulta em 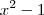 . Portanto, temos que
. Portanto, temos que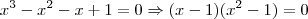


 .
.
 :
: