 por [+-++-+] » Ter Abr 12, 2011 13:55
por [+-++-+] » Ter Abr 12, 2011 13:55
Determine o valor de X, sabendo que o triângulo de vértices A (1,-2), B (x,4) e C (0,6) é retângulo em A.
Gostaria de saber se a resposta esta certa x= 49
Eu comecei por Pitágoras
Editado pela última vez por
[+-++-+] em Ter Abr 12, 2011 21:28, em um total de 1 vez.
-
[+-++-+]
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 11, 2011 14:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Ter Abr 12, 2011 14:11
por LuizAquino » Ter Abr 12, 2011 14:11
Dica
Queremos que o triângulo ABC seja retângulo em B. Portanto, você pode conferir a sua resposta verificando se AB é perpendicular a BC.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por [+-++-+] » Ter Abr 12, 2011 21:44
por [+-++-+] » Ter Abr 12, 2011 21:44
LuizAquino escreveu:Dica
Queremos que o triângulo ABC seja retângulo em B. Portanto, você pode conferir a sua resposta verificando se AB é perpendicular a BC.
Luiz Valeu
Eu tinha digitado a questão errada mais acabei de corrigi teria como vc verificar se esta certa essa questão
Retângulo em A, BC é a hipotenusa
BC² = AC² + BA²
BC= x²+4
AC= 65
BA= x²-2x+37
LOGO
x²+4=65+x²-2x+37
x=49
Estaria certo
fico no seu aguardo ou de outro colaborador
-
[+-++-+]
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 11, 2011 14:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qua Abr 13, 2011 10:18
por LuizAquino » Qua Abr 13, 2011 10:18
Dados os pontos P=(x0, y0) e Q=(x, y), sabemos que a distância entre esses pontos será:

Refaça o exercício lembrando-se disso.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por [+-++-+] » Qui Abr 14, 2011 21:58
por [+-++-+] » Qui Abr 14, 2011 21:58
LuizAquino escreveu:Dados os pontos P=(x0, y0) e Q=(x, y), sabemos que a distância entre esses pontos será:

Refaça o exercício lembrando-se disso.
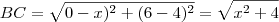
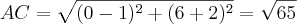
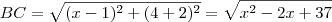
Luiz o caminho seria esse
Fico no seu aguardo
-
[+-++-+]
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 11, 2011 14:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por FilipeCaceres » Qui Abr 14, 2011 22:28
por FilipeCaceres » Qui Abr 14, 2011 22:28
Se o teu triangulo for retângulo em A,tendo calculado o valor das distâncias basta agora fazer,
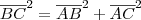
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por [+-++-+] » Sex Abr 15, 2011 13:54
por [+-++-+] » Sex Abr 15, 2011 13:54
filipecaceres escreveu:Se o teu triangulo for retângulo em A,tendo calculado o valor das distâncias basta agora fazer,
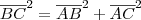
Abraço.
Logo
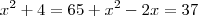
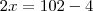

Luiz
Estaria correto
Desde já muito obrigado
Fique com Deus
-
[+-++-+]
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Abr 11, 2011 14:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Analítica
por maysa » Ter Abr 14, 2009 10:35
- 1 Respostas
- 7693 Exibições
- Última mensagem por Marcampucio

Ter Abr 14, 2009 15:52
Geometria Analítica
-
- GEOMETRIA ANALITICA
por GABRIELA » Ter Set 29, 2009 17:20
- 3 Respostas
- 5453 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 16:49
Geometria Analítica
-
- Geometria analítica
por shirata » Qua Nov 11, 2009 20:37
- 2 Respostas
- 4182 Exibições
- Última mensagem por shirata

Dom Nov 15, 2009 09:25
Geometria Espacial
-
- geometria analitica
por Jaison Werner » Sex Abr 23, 2010 21:19
- 3 Respostas
- 3961 Exibições
- Última mensagem por MarceloFantini

Dom Jun 13, 2010 19:03
Geometria Analítica
-
- geometria analitica
por Jaison Werner » Qui Abr 29, 2010 20:44
- 1 Respostas
- 2795 Exibições
- Última mensagem por MarceloFantini

Qui Abr 29, 2010 21:10
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.







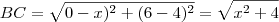
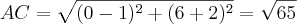
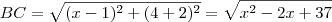

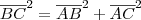

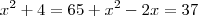
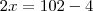


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.