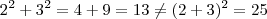por will » Qui Abr 07, 2011 01:30
por will » Qui Abr 07, 2011 01:30
Gostaria de uma ajuda para resolver esta equação: 100000-1,46^m = 30000x1,04^m
Ja tentei por várias horas e não consigo resolvê-la.
Alguém poderia me orientar?
Obrigado!
-
will
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Abr 06, 2011 20:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Regina » Dom Abr 10, 2011 13:33
por Regina » Dom Abr 10, 2011 13:33
Boa tarde
Se for esta a expressão
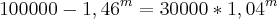
é fácil de resolver.
Eu fiz da eguinte forma:
1)
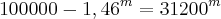
2)
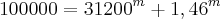
3)
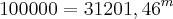
Agora transforma a base do expoente em logaritmo
4)
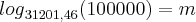
como as calculadoras só calculam logaritmos de base 10 ou base e, basta fazer uma mudança de base de acordo com:
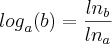
5)
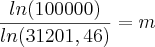
Coloca tudo na calculadora e vai lhe dar o resultado de m
6)
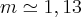
Confirme o resultado
Ajudei?
-
Regina
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Sex Fev 25, 2011 14:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso técnico em química
- Andamento: cursando
 por Molina » Dom Abr 10, 2011 18:34
por Molina » Dom Abr 10, 2011 18:34
Boa tarde, Regina!
Há algumas passagens erradas no seu desenvolvimento, veja:
Regina escreveu:Boa tarde
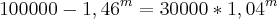
1)
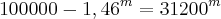
Você considerou que
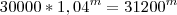
. Isto não é verdade. Perceba pelo exemplo mais fácil:

Outra passagem equivocada sua é
Regina escreveu:2)
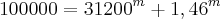
3)
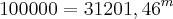
Outro exemplo simples de mostrar o erro:
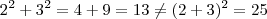

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Fabricio dalla » Dom Abr 10, 2011 20:44
por Fabricio dalla » Dom Abr 10, 2011 20:44
vc so poderia multiplicar 3000.1,04 elevado a m se 3000 fosse elevado a m tbm
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função exponencial] Exercício sobre função exponencial
por fff » Ter Jan 07, 2014 17:51
- 3 Respostas
- 4073 Exibições
- Última mensagem por fff

Qua Jan 08, 2014 06:47
Funções
-
- [Desigualdade] entre função exponencial e função potência
por VitorFN » Sex Mai 26, 2017 15:18
- 1 Respostas
- 5745 Exibições
- Última mensagem por adauto martins

Sex Jul 07, 2017 12:17
Álgebra Elementar
-
- [função exponencial] Exprimir em função de x
por fff » Ter Jan 07, 2014 12:02
- 2 Respostas
- 3127 Exibições
- Última mensagem por fff

Ter Jan 07, 2014 13:23
Funções
-
- funçao exponencial ITA
por zeramalho2004 » Dom Jun 28, 2009 19:55
- 3 Respostas
- 5118 Exibições
- Última mensagem por Marcampucio

Seg Jun 29, 2009 15:23
Funções
-
- Função Exponencial
por Aline » Seg Jun 29, 2009 18:59
- 3 Respostas
- 5901 Exibições
- Última mensagem por Cleyson007

Qua Jul 01, 2009 22:59
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



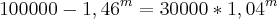 é fácil de resolver.
é fácil de resolver.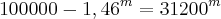
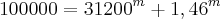
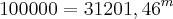
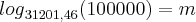
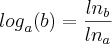
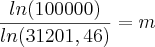
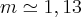

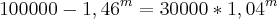
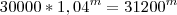 . Isto não é verdade. Perceba pelo exemplo mais fácil:
. Isto não é verdade. Perceba pelo exemplo mais fácil: