Estamos estudando em dupla para os vestibulares no fim de ano, nos deparamos com um problema que diz o seguinte: "Considere-se o conjunto M de todos os números inteiros formados por exatamente três algarismos iguais. Pode-se afirmar que todo n ? M é múltiplo de: a) 5; b) 7; c) 13; d) 17 ou e) 37.
Fazendo as contas com base nas opções de respostas, encontramos a solução "e)37". Porém a dúvida é quais números representam o "n", eu entendo que são tão somente: 111; 222; 333; 444; 555; 666; 777; 888 e 999. Mas o outro estudante acredita que seja todos os números múltiplos de 37. Quais números estão representando o "n"?


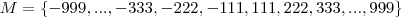


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)