 por LausDeo » Sáb Mar 26, 2011 13:59
por LausDeo » Sáb Mar 26, 2011 13:59
Estamos estudando em dupla para os vestibulares no fim de ano, nos deparamos com um problema que diz o seguinte: "Considere-se o conjunto M de todos os números inteiros formados por exatamente três algarismos iguais. Pode-se afirmar que todo n ? M é múltiplo de: a) 5; b) 7; c) 13; d) 17 ou e) 37.
Fazendo as contas com base nas opções de respostas, encontramos a solução "e)37". Porém a dúvida é quais números representam o "n", eu entendo que são tão somente: 111; 222; 333; 444; 555; 666; 777; 888 e 999. Mas o outro estudante acredita que seja todos os números múltiplos de 37. Quais números estão representando o "n"?
-
LausDeo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mar 26, 2011 13:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico RH
- Andamento: cursando
 por FilipeCaceres » Sáb Mar 26, 2011 14:49
por FilipeCaceres » Sáb Mar 26, 2011 14:49
Vamos interpretar o enunciado:
Considere-se o conjunto M de todos os números INTEIROS formados por exatamente três algarismos iguais.
Logo,
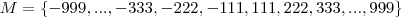
Se n ? M, então, n é um número que pertence ao conjunto M, e não todos os multiplos de 37, pois 148 é multiplo e não está no conjunto.
Sabendo como o conjunto é formado acredito que seja suficiente para achar a resposta.
Qualquer dúvido é só perguntar.
Abraço
Editado pela última vez por
FilipeCaceres em Sáb Mar 26, 2011 15:09, em um total de 2 vezes.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por LuizAquino » Sáb Mar 26, 2011 15:06
por LuizAquino » Sáb Mar 26, 2011 15:06
"Considere-se o conjunto M de todos os números inteiros formados por exatamente três algarismos iguais"
Isso quer dizer que qualquer elemento x pertencente a M tem o formato: x = 100a+10a+a, onde a é inteiro e -10 < a <10.
Desse modo, temos que x=111a. Como 111 é um múltiplo de 37, então x também é múltiplo desse número.
Portanto, podemos afirmar que qualquer elemento do conjunto M é um múltiplo de 37.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por LausDeo » Sáb Mar 26, 2011 15:37
por LausDeo » Sáb Mar 26, 2011 15:37
Vendo as duas respostas, entendi que há divergências, pois a primeira limita os conjunto M, somente em "-999, 888, 777, ... ..., 888 e 999. A segunda resposta dia que todo múltiplo de 37 pertence ao M.
O que é verdade...?
-
LausDeo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Mar 26, 2011 13:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico RH
- Andamento: cursando
 por LuizAquino » Sáb Mar 26, 2011 15:48
por LuizAquino » Sáb Mar 26, 2011 15:48
LausDeo escreveu: A segunda resposta diz que todo múltiplo de 37 pertence ao M.
Dizer que "todo múltiplo de 37 pertence a M" não é a mesma coisa de dizer que "qualquer elemento do conjunto M é um múltiplo de 37" (que foi o que eu disse). Tenha mais cuidado com a leitura.
Vamos a pergunta do exercício:
Pode-se afirmar que todo n ? M é múltiplo de:
a) 5
b) 7
c) 13
d) 17
e) 37
Perceba que
não há a afirmação no exercício de que M deve ser
igual ao conjunto dos múltiplos dos números das alternativas. O exercício quer apenas saber se qualquer elemento de M pode ser um múltiplo dos números nas alternativas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Conjuntos] Confusão em teoria dos conjuntos numa questão.
 por Debora Bruna » Seg Jan 11, 2016 17:44
por Debora Bruna » Seg Jan 11, 2016 17:44
- 1 Respostas
- 8842 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 23, 2016 16:44
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6422 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- [conjuntos]numeros racionais e conjuntos
por fenixxx » Ter Fev 28, 2012 21:35
- 3 Respostas
- 4731 Exibições
- Última mensagem por DanielFerreira

Sex Mar 02, 2012 00:04
Álgebra Elementar
-
- [Conjuntos] Problema de conjuntos com porcentagem
por Tibes » Qui Jan 31, 2013 14:29
- 1 Respostas
- 7959 Exibições
- Última mensagem por young_jedi

Sex Fev 01, 2013 12:39
Conjuntos
-
- [Conjuntos] Conjuntos e geometria plana
por bencz » Dom Mar 03, 2013 12:58
- 3 Respostas
- 11208 Exibições
- Última mensagem por maison_souza

Sex Nov 14, 2014 13:15
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


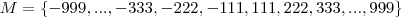




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.