![\sqrt[n]{u^n}= |u| \sqrt[n]{u^n}= |u|](/latexrender/pictures/54074dbf32e9df1934b83de0fb12d607.png) para n par.
para n par.Aí vem a minha dúvida:
![\sqrt[]{2^2} \sqrt[]{2^2}](/latexrender/pictures/961bbba4cf8385e83c200e77775105dc.png) não seria +-2? Então por que a propriedade diz que o resultado é módulo de u?
não seria +-2? Então por que a propriedade diz que o resultado é módulo de u?
![\sqrt[n]{u^n}= |u| \sqrt[n]{u^n}= |u|](/latexrender/pictures/54074dbf32e9df1934b83de0fb12d607.png) para n par.
para n par.![\sqrt[]{2^2} \sqrt[]{2^2}](/latexrender/pictures/961bbba4cf8385e83c200e77775105dc.png) não seria +-2? Então por que a propriedade diz que o resultado é módulo de u?
não seria +-2? Então por que a propriedade diz que o resultado é módulo de u?

Elcioschin escreveu:Por definição:
O valor \/(2²) NÃO pode ser +2 e -2 ----> O valor é 2 ou |2|
![\sqrt[4]{16}=+-2 \sqrt[4]{16}=+-2](/latexrender/pictures/a3634d1648072dd5b178583dbe671b36.png)

renanrdaros escreveu:Aí vem a minha dúvida:não seria +-2? Então por que a propriedade diz que o resultado é módulo de u?
 , que é
, que é 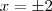 com o valor de
com o valor de 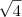 , que é 2.
, que é 2.![\sqrt[n]{u^n}= |u| \sqrt[n]{u^n}= |u|](/latexrender/pictures/54074dbf32e9df1934b83de0fb12d607.png) , para n par.
, para n par.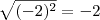 .
. .
. .
.renanrdaros escreveu:Esse é o problema. O livro afirma a existência dessa propriedade, mas também afirma que
 ?
? 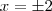 .
.![\sqrt[4]{16} \sqrt[4]{16}](/latexrender/pictures/3d348a2f5f00b0a55c947d53f10550ad.png) , então o resultado é 2.
, então o resultado é 2.
![\sqrt[4]{16}=\pm 2 \sqrt[4]{16}=\pm 2](/latexrender/pictures/7eaf9c81aff332d3b90bd7d89141da95.png)

![\sqrt[n]{a} \sqrt[n]{a}](/latexrender/pictures/bf7ff33f3b129b15c06203d60f007807.png) ".
".![\sqrt[4]{16}=\pm 2 \sqrt[4]{16}=\pm 2](/latexrender/pictures/7eaf9c81aff332d3b90bd7d89141da95.png) .
. ![\sqrt[n]{a} \sqrt[n]{a}](/latexrender/pictures/bf7ff33f3b129b15c06203d60f007807.png) denota a raiz principal de a. Além disso, ele define que a "principal raiz n-ésima de a é aquela com o mesmo sinal de a". Portanto,
denota a raiz principal de a. Além disso, ele define que a "principal raiz n-ésima de a é aquela com o mesmo sinal de a". Portanto, ![\sqrt[4]{16} \sqrt[4]{16}](/latexrender/pictures/3d348a2f5f00b0a55c947d53f10550ad.png) denota a principal raiz quarta de 16, que é 2. Ou seja, Devemos escrever
denota a principal raiz quarta de 16, que é 2. Ou seja, Devemos escrever ![\sqrt[4]{16} = 2 \sqrt[4]{16} = 2](/latexrender/pictures/bacfd714cdc4d603b6797264000c27ea.png) .
.
![\sqrt[]{2x^3y^4}=\sqrt[]{(xy^2)^2.2x}=\sqrt[]{(xy^2)^2} . \sqrt[]{2x}=|x|y^2\sqrt[]{2x} \sqrt[]{2x^3y^4}=\sqrt[]{(xy^2)^2.2x}=\sqrt[]{(xy^2)^2} . \sqrt[]{2x}=|x|y^2\sqrt[]{2x}](/latexrender/pictures/7d1e52fbbdd2c3418a9eb856962e56ae.png)

 , para qualquer número real a.
, para qualquer número real a.


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.



