Estou resolvendo um problema de física e travei na álgebra. Já tentei desenvolver os produtos notáveis, mas não consegui eliminar o termo b.
Como posso eliminar o termo b em

quero deixar apenas em função de a
[]s



mvww escreveu:Estou resolvendo um problema de física e travei na álgebra. Já tentei desenvolver os produtos notáveis, mas não consegui eliminar o termo b.
Como posso eliminar o termo b em
quero deixar apenas em função de a
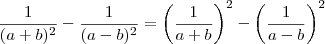
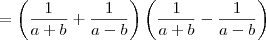
![= \left[\frac{(a-b)+(a+b)}{(a+b)(a-b)}\right]\left[\frac{(a-b)-(a+b)}{(a+b)(a-b)}\right] = \left[\frac{(a-b)+(a+b)}{(a+b)(a-b)}\right]\left[\frac{(a-b)-(a+b)}{(a+b)(a-b)}\right]](/latexrender/pictures/57cc1c4ce0aaed233dbfe2dd475f116c.png)
![= \left[\frac{2a}{(a+b)(a-b)}\right]\left[\frac{-2b}{(a+b)(a-b)}\right] = \left[\frac{2a}{(a+b)(a-b)}\right]\left[\frac{-2b}{(a+b)(a-b)}\right]](/latexrender/pictures/1a5bc0f28485a259937ea23b1f3b7fa9.png)
![= -\frac{4ab}{[(a+b)(a-b)]^2} = -\frac{4ab}{[(a+b)(a-b)]^2}](/latexrender/pictures/43177a1beb9d9dd0816428505c311dff.png)

LuizAquino escreveu:mvww escreveu:Estou resolvendo um problema de física e travei na álgebra. Já tentei desenvolver os produtos notáveis, mas não consegui eliminar o termo b.
Como posso eliminar o termo b em
quero deixar apenas em função de a
Assim do jeito que está não há como eliminar o termo b. Veja o desenvolvimento abaixo.


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)