 por Raphael Feitas10 » Qua Mar 16, 2011 01:19
por Raphael Feitas10 » Qua Mar 16, 2011 01:19
Uma pessoa deu 2/5 do que possuia e, em seguida emprestou 1/3 do resto.Calcule a razão entre o que ela possuia e o resto final.R:2/5
cheguei ate aqui mas ñ achei me ajuda aew parceiro...
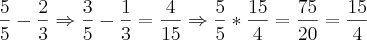
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Mar 16, 2011 09:33
por LuizAquino » Qua Mar 16, 2011 09:33
Se a pessoa tinha
x e deu 2/5, então ela ficou com
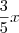
.
Se agora ela tem
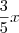
e emprestou 1/3, então ela ficou com
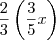
.
Agora é fácil terminar o exercício!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Raphael Feitas10 » Qua Mar 16, 2011 13:32
por Raphael Feitas10 » Qua Mar 16, 2011 13:32
Como vc achou esse 2/3, ñ entendie mesmo resolvendo aqui achei 9x=10 que fica x=10/9 ou se eliminar os dois 3 aew fica 2/5 só se for assim me tira essa duvida aew por favor parceiro...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por LuizAquino » Qua Mar 16, 2011 14:07
por LuizAquino » Qua Mar 16, 2011 14:07
Imagine que você tem um objeto inteiro. Agora, imagine que você vai retirar 1/3 desse objeto. Quanto irá sobrar desse objeto? Ora, irá sobrar 2/3.
Em relação à última operação, eu tenho uma pergunta para você: como se multiplica frações? Perceba que o que você tem é a multiplicação da fração 2/3 pela fração 3/5.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Raphael Feitas10 » Qui Mar 17, 2011 13:35
por Raphael Feitas10 » Qui Mar 17, 2011 13:35
Entendie ja brother vc tirou 1/3 do todo q é 3/3 né isso,e no caso da aperação só é mutiplicar q no caso vai da 6/15 que simplificando dá 2/5 valeu muito obrg pela ajuda parceiro...
-
Raphael Feitas10
- Colaborador Voluntário

-
- Mensagens: 162
- Registrado em: Ter Jan 04, 2011 20:10
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- RAZÃO
por hevhoram » Qua Jun 02, 2010 11:50
- 1 Respostas
- 1544 Exibições
- Última mensagem por Molina

Qua Jun 02, 2010 18:43
Álgebra Elementar
-
- razao
por hevhoram » Qua Jun 02, 2010 20:14
- 2 Respostas
- 1686 Exibições
- Última mensagem por hevhoram

Qui Jun 03, 2010 20:42
Álgebra Elementar
-
- Razão
por Guaciara » Qui Set 23, 2010 22:40
- 2 Respostas
- 2416 Exibições
- Última mensagem por Guaciara

Qui Set 23, 2010 23:31
Conversão de Unidades
-
- razão
por angeloka » Sex Out 15, 2010 19:29
- 8 Respostas
- 6809 Exibições
- Última mensagem por MarceloFantini

Sáb Out 23, 2010 01:41
Álgebra Elementar
-
- PA com razão 0,3
por gustavowelp » Sex Nov 19, 2010 08:42
- 5 Respostas
- 3463 Exibições
- Última mensagem por 0 kelvin

Sex Nov 19, 2010 15:51
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
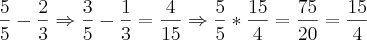

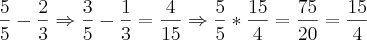

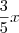 .
.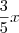 e emprestou 1/3, então ela ficou com
e emprestou 1/3, então ela ficou com 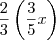 .
.





 , avisa que eu resolvo.
, avisa que eu resolvo.

