 por Amd » Sex Mar 11, 2011 22:29
por Amd » Sex Mar 11, 2011 22:29
Meu professor mandou um exercico muito complexo e ñ consigo resolver por favor alguem me ajuda
Os coeficientes a, b, c da equação de 2º grau ax^2 + bx + c = 0 são nessa ordem, termos de uma P.A. de razão 2.
A) Mostre que essa equação admite raizes reais para exatamente 4 valores inteiros de b, determinando-os.
B) Para cada valor encontrado no item anterior, determine raizes da equação.
-
Amd
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Mar 11, 2011 22:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Abelardo » Sex Mar 11, 2011 23:41
por Abelardo » Sex Mar 11, 2011 23:41
A equação é da seguinte forma:
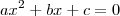
Como os coeficientes formam na ordem
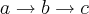
uma P.A. de razão 2, podemos fazer o seguinte -->
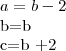
Substitua nos coeficientes a e c os valores correspondentes e determine a discriminante.. encontrarás como resultada dessa uma outra equação
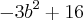
. Lembrando que valores menores que zero para discriminante não há raízes reais, logo
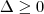
. Quando desenvolveres a desigualdade perceberás que os valores de b serão -
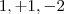
e
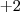
. Substitua esses valores lá na primeira equação e encontrarás 4 equações diferentes. veja quais delas são realmente de segundo grau e depois determine as raízes.. Fiz assim e consegui, mas pode haver um método mais simples ou posso ter errado em algum cálculo e ter me precipitado, bom, espero que consiga!
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Abelardo » Sáb Mar 12, 2011 02:52
por Abelardo » Sáb Mar 12, 2011 02:52
Sempre existe uma solução diferente, mais simples, deixei até um comentário no final da minha resolução kkk. Foi linda essa resolução sua!
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- PRECISO DE AJUDA !
por Layna Cardoso » Ter Mar 16, 2010 20:49
- 1 Respostas
- 2022 Exibições
- Última mensagem por Molina

Ter Mar 16, 2010 21:37
Problemas do Cotidiano
-
- PRECISO DE AJUDA!
por Lurdes » Sex Jul 09, 2010 23:22
- 1 Respostas
- 3425 Exibições
- Última mensagem por Neperiano

Qui Set 29, 2011 16:45
Problemas do Cotidiano
-
- preciso de ajuda...
por apoliveirarj » Qua Jul 21, 2010 12:25
- 5 Respostas
- 4187 Exibições
- Última mensagem por apoliveirarj

Qui Jul 22, 2010 12:52
Sistemas de Equações
-
- preciso de ajuda...
por apoliveirarj » Sáb Jul 24, 2010 19:10
- 1 Respostas
- 3054 Exibições
- Última mensagem por Neperiano

Sex Set 17, 2010 15:00
Estatística
-
- preciso de ajuda:
por angeloka » Ter Out 05, 2010 23:00
- 1 Respostas
- 2156 Exibições
- Última mensagem por MarceloFantini

Ter Out 05, 2010 23:39
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


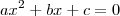
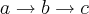 uma P.A. de razão 2, podemos fazer o seguinte -->
uma P.A. de razão 2, podemos fazer o seguinte --> 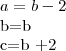
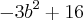 . Lembrando que valores menores que zero para discriminante não há raízes reais, logo
. Lembrando que valores menores que zero para discriminante não há raízes reais, logo 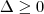 . Quando desenvolveres a desigualdade perceberás que os valores de b serão -
. Quando desenvolveres a desigualdade perceberás que os valores de b serão -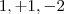 e
e 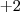 . Substitua esses valores lá na primeira equação e encontrarás 4 equações diferentes. veja quais delas são realmente de segundo grau e depois determine as raízes.. Fiz assim e consegui, mas pode haver um método mais simples ou posso ter errado em algum cálculo e ter me precipitado, bom, espero que consiga!
. Substitua esses valores lá na primeira equação e encontrarás 4 equações diferentes. veja quais delas são realmente de segundo grau e depois determine as raízes.. Fiz assim e consegui, mas pode haver um método mais simples ou posso ter errado em algum cálculo e ter me precipitado, bom, espero que consiga!
 não seria uma escolha interessante? Atende ao discriminante e continua sendo uma equação de segundo grau. Talvez quem montou o exercício imaginou a P.A. na forma
não seria uma escolha interessante? Atende ao discriminante e continua sendo uma equação de segundo grau. Talvez quem montou o exercício imaginou a P.A. na forma  ,
, 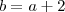 e
e 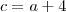 .
.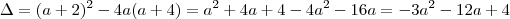
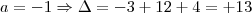
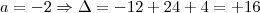
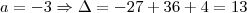
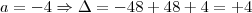
 pois senão não há equação do segundo grau. Com
pois senão não há equação do segundo grau. Com 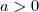 , o discriminante é menor que zero e portanto não tem raízes reais. Com
, o discriminante é menor que zero e portanto não tem raízes reais. Com 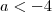 , discriminante volta a ser negativo, logo, existem somente 4 valores inteiros tais que a equação tenha solução.
, discriminante volta a ser negativo, logo, existem somente 4 valores inteiros tais que a equação tenha solução.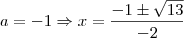
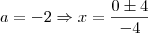
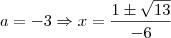
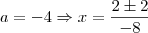




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.