resp.:
![2\sqrt[]{5}](/latexrender/pictures/8afe59aad7560ad383eefaf7fd49cdb9.png "2\sqrt[]{5}")
Essa eu consegui fazer mas estou com dúvida se usei o caminho certo ou mais curto.
Eu fiz assim:
Encotrei a distância entre o centro da circunferência P(3,4) e a reta (x+2y = 1). Prá isso usei essa fórmula.
d(P,r) =
![\frac{\left|ax+by+c \right|}{\sqrt[]{{a}^{2}+{b}^{2}}}](/latexrender/pictures/0932dfd3e31795311f9b2ae064b66444.png "\frac{\left|ax+by+c \right|}{\sqrt[]{{a}^{2}+{b}^{2}}}")
= ![\frac{\left|-\frac{1}{2}3-1*4+\frac{1}{2} \right|}{\sqrt[]{{\left(-\frac{1}{2} \right)}^{2}+{\left(-1 \right)}^{2}}}](/latexrender/pictures/924e8b03aaa4668a34765f00bc28a9be.png "\frac{\left|-\frac{1}{2}3-1*4+\frac{1}{2} \right|}{\sqrt[]{{\left(-\frac{1}{2} \right)}^{2}+{\left(-1 \right)}^{2}}}")
= Eu queria saber se o caminho tá bom ou teria um mais rápido no concurso?
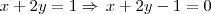
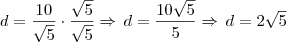
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)