
a) Determine a secção desse plano com o cubo.
b) Considere que a medida da aresta do cubo seja a .
Calcule a área dessa secção em função de a .
c) Encontre três pontos (sobre as arestas do cubo) que
determinam um plano que seccione o cubo, em um trapézio
isósceles.
RESPOSTAS:
A)

B)
A/2...???????
C)
 ?????????????????????????
?????????????????????????2) Um sólido de revolução, obtido pela rotação de uma figura F ao redor de um eixo e , resulta em um cone circular reto e um cilindro circular reto, como na ilustração.

a) Determine a posição do eixo na figura ao lado e a área de F em função do raio R, sabendo que as geratrizes do cone e do cilindro medem o triplo de R.
b) Determine o valor de R de modo que a secção por um plano que contenha o eixo e tenha área igual a 12 cm2.
RESPOSTAS:
A) se a região é um triangulo retangulo com base no eixo x e 2 verteces nos ponto (a,0) e (b,0) com angulo reto, então o eixo é vertical.
Area total =
 * r (g+r)
* r (g+r)Area total = 3,14 * r(3r+r)
Area total = 3,14 * 5r
Area total = 15,70r
b) 12 = 15,70r
12 = r
15,70
r = 0,76
Por favor, me ajudem.


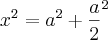 ( observe que para determinar o lado NP, ele é a hipotenusa de um triângulo com catetos NA e PA. Logo, nessa equação, procuramos o valor de PA... consegue ver esse triângulo)!
( observe que para determinar o lado NP, ele é a hipotenusa de um triângulo com catetos NA e PA. Logo, nessa equação, procuramos o valor de PA... consegue ver esse triângulo)!![x=\frac{a \sqrt[] {5}}{4} x=\frac{a \sqrt[] {5}}{4}](/latexrender/pictures/504e470ba67aaee0a941546492a7c0b4.png)
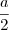 e PA=
e PA=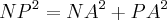
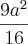 .
.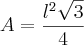 .
.![\frac{9{a}^{2}\sqrt[]{3}}{64} \frac{9{a}^{2}\sqrt[]{3}}{64}](/latexrender/pictures/4d3addd37603cdcacaeee3460349dbd9.png) . Tá ai a letra B.
. Tá ai a letra B.