Desde já agradeço.
Ai vai o exercício:










![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1}](/latexrender/pictures/576963920200cdc441033bc34d5a93e2.png)
![u = \sqrt[n]{x} u = \sqrt[n]{x}](/latexrender/pictures/e761d73d2c35c550efb26912c17251fc.png) , obtendo assim um novo limite (note que u também tenderá a 1):
, obtendo assim um novo limite (note que u também tenderá a 1):![\lim_{u\to 1}\frac{\sqrt[m]{u^n} - 1}{u - 1} \lim_{u\to 1}\frac{\sqrt[m]{u^n} - 1}{u - 1}](/latexrender/pictures/73a18bc8ba53226ac4b8dd6777ede4f6.png)
![\lim_{u\to 1}\frac{\left(\sqrt[m]{u}\right)^n - 1^n}{\left(\sqrt[m]{u}\right)^m - 1^m} \lim_{u\to 1}\frac{\left(\sqrt[m]{u}\right)^n - 1^n}{\left(\sqrt[m]{u}\right)^m - 1^m}](/latexrender/pictures/d68aa5ece324b8b9baa8ef25900e34e3.png)
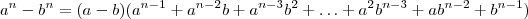 :
:![\lim_{u\to 1}\frac{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)}{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)} \lim_{u\to 1}\frac{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)}{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)}](/latexrender/pictures/3f82820018e577a813531ec52cdb279d.png)
![\lim_{u\to 1}\frac{\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1}{\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1} \lim_{u\to 1}\frac{\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1}{\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1}](/latexrender/pictures/325e2d24ba59a30523c090e16a4666cc.png)
![\sqrt[m]{x}^k \sqrt[m]{x}^k](/latexrender/pictures/0e3cdc1b624d04beb3b97666dc34a824.png) (com k=n-1, n-2, ..., 1) no numerador será igual a 1. Quantos desses termos nós temos? Nós temos n-1 desses termos. Já no denominador nós temos m-1 termos do tipo
(com k=n-1, n-2, ..., 1) no numerador será igual a 1. Quantos desses termos nós temos? Nós temos n-1 desses termos. Já no denominador nós temos m-1 termos do tipo ![\sqrt[m]{x}^k \sqrt[m]{x}^k](/latexrender/pictures/0e3cdc1b624d04beb3b97666dc34a824.png) (com k=m-1, m-2, ..., 1).
(com k=m-1, m-2, ..., 1).![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} = \frac{(n-1)\cdot 1 + 1}{(m-1)\cdot 1 + 1} = \frac{n}{m} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} = \frac{(n-1)\cdot 1 + 1}{(m-1)\cdot 1 + 1} = \frac{n}{m}](/latexrender/pictures/2860d5a3ad57911cf300be5e313538d5.png)


![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1}](/latexrender/pictures/576963920200cdc441033bc34d5a93e2.png) . Substituindo x por 1 temos uma indeterminação do tipo
. Substituindo x por 1 temos uma indeterminação do tipo  . Sendo assim, podemos usar a regra de L'Hopital que nada mais é do que derivar o numerador e derivar o denominador (separadamente) e posteriormente calcular o limite:
. Sendo assim, podemos usar a regra de L'Hopital que nada mais é do que derivar o numerador e derivar o denominador (separadamente) e posteriormente calcular o limite:![\lim_{x\to 1}\frac{(\sqrt[m]{x} - 1)'}{(\sqrt[n]{x} - 1)'}=\lim_{x\to 1}\frac{\frac{1}{m}*x^{\frac{1-m}{m}}}{\frac{1}{n}*x^{\frac{1-n}{n}}}=\frac{\frac{1}{m}}{\frac{1}{n}}=\frac{n}{m} \lim_{x\to 1}\frac{(\sqrt[m]{x} - 1)'}{(\sqrt[n]{x} - 1)'}=\lim_{x\to 1}\frac{\frac{1}{m}*x^{\frac{1-m}{m}}}{\frac{1}{n}*x^{\frac{1-n}{n}}}=\frac{\frac{1}{m}}{\frac{1}{n}}=\frac{n}{m}](/latexrender/pictures/310cc61e1e78b2be8ed8d8ae85a6d2e1.png)


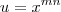 , pois desse modo o limite ficaria bem simples:
, pois desse modo o limite ficaria bem simples: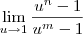

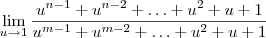
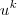 n-1 vezes no numerador e m-1 vezes no denominador, novamente o limite original é equivalente a:
n-1 vezes no numerador e m-1 vezes no denominador, novamente o limite original é equivalente a:![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} = \frac{(n-1)\cdot 1 + 1}{(m-1)\cdot 1 + 1} = \frac{n}{m} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} = \frac{(n-1)\cdot 1 + 1}{(m-1)\cdot 1 + 1} = \frac{n}{m}](/latexrender/pictures/2860d5a3ad57911cf300be5e313538d5.png)


vdzz escreveu:Esse seu segundo exemplo Luiz, achei mais tranquilo comparado ao primeiro.

LuizAquino escreveu:Para aguçar ainda mais a curiosidade sobre esse exercício, poderíamos fazer ainda uma substituição bem elegante, que seria fazer, pois desse modo o limite ficaria bem simples:
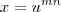 e não
e não 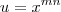 como foi escrito anteriormente.
como foi escrito anteriormente.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes