 por vdzz » Qua Fev 16, 2011 17:15
por vdzz » Qua Fev 16, 2011 17:15
Olá, alguém poderia me ajudar com este exercício, explicando passo a passo e se possível passar algum outro para eu tentar fazer ?
Desde já agradeço.
Ai vai o exercício:

-
vdzz
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Fev 16, 2011 17:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por Molina » Qua Fev 16, 2011 17:19
por Molina » Qua Fev 16, 2011 17:19
Boa tarde.
Por favor, coloque o enunciado completo da questão.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por vdzz » Qua Fev 16, 2011 17:37
por vdzz » Qua Fev 16, 2011 17:37
A questão é achar o limite de x, naquela função.
-
vdzz
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Fev 16, 2011 17:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por Molina » Qua Fev 16, 2011 18:19
por Molina » Qua Fev 16, 2011 18:19
Fiz usando L`Hopital, é válido?
Possa até ter outro método, mas usando este procedimento sai em 3 linhas...
A resposta deu


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por vdzz » Qua Fev 16, 2011 18:48
por vdzz » Qua Fev 16, 2011 18:48
Creio que sim.
Tem como você me explicar esse procedimento e me explicar passo a passo como você fez?
No exemplo em que a professora deu, ela usou substituição.
-
vdzz
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Fev 16, 2011 17:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por LuizAquino » Qua Fev 16, 2011 19:18
por LuizAquino » Qua Fev 16, 2011 19:18
Seja o limite:
![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1}](/latexrender/pictures/576963920200cdc441033bc34d5a93e2.png)
Façamos a substituição
![u = \sqrt[n]{x} u = \sqrt[n]{x}](/latexrender/pictures/e761d73d2c35c550efb26912c17251fc.png)
, obtendo assim um novo limite (note que u também tenderá a 1):
![\lim_{u\to 1}\frac{\sqrt[m]{u^n} - 1}{u - 1} \lim_{u\to 1}\frac{\sqrt[m]{u^n} - 1}{u - 1}](/latexrender/pictures/73a18bc8ba53226ac4b8dd6777ede4f6.png)
Arrumando de forma conveniente:
![\lim_{u\to 1}\frac{\left(\sqrt[m]{u}\right)^n - 1^n}{\left(\sqrt[m]{u}\right)^m - 1^m} \lim_{u\to 1}\frac{\left(\sqrt[m]{u}\right)^n - 1^n}{\left(\sqrt[m]{u}\right)^m - 1^m}](/latexrender/pictures/d68aa5ece324b8b9baa8ef25900e34e3.png)
Usando o produto notável
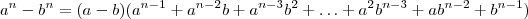
:
![\lim_{u\to 1}\frac{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)}{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)} \lim_{u\to 1}\frac{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)}{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)}](/latexrender/pictures/3f82820018e577a813531ec52cdb279d.png)
![\lim_{u\to 1}\frac{\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1}{\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1} \lim_{u\to 1}\frac{\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1}{\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1}](/latexrender/pictures/325e2d24ba59a30523c090e16a4666cc.png)
Não há mais indeterminação! Fazendo u tender a 1, temos que cada
![\sqrt[m]{x}^k \sqrt[m]{x}^k](/latexrender/pictures/0e3cdc1b624d04beb3b97666dc34a824.png)
(com k=n-1, n-2, ..., 1) no numerador será igual a 1. Quantos desses termos nós temos? Nós temos n-1 desses termos. Já no denominador nós temos m-1 termos do tipo
![\sqrt[m]{x}^k \sqrt[m]{x}^k](/latexrender/pictures/0e3cdc1b624d04beb3b97666dc34a824.png)
(com k=m-1, m-2, ..., 1).
Portanto, o limite original é equivalente há:
![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} = \frac{(n-1)\cdot 1 + 1}{(m-1)\cdot 1 + 1} = \frac{n}{m} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} = \frac{(n-1)\cdot 1 + 1}{(m-1)\cdot 1 + 1} = \frac{n}{m}](/latexrender/pictures/2860d5a3ad57911cf300be5e313538d5.png)
Obviamente, como indicou o colega Molina, usando a regra de L'Hôpital o exercício sai em poucas linhas. Mas, partindo do pressuposto que a pessoa ainda não tenha estudado derivada, essa regra não poderia ser aplicada. De qualquer modo, segue aqui a solução sem usar essa regra.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vdzz » Qua Fev 16, 2011 20:48
por vdzz » Qua Fev 16, 2011 20:48
Valeu luiz.
-
vdzz
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Fev 16, 2011 17:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por Molina » Qua Fev 16, 2011 20:54
por Molina » Qua Fev 16, 2011 20:54
Perfeita a solução so Luiz Aquino.
Mas para adiantar provavelmente o assunto que você estudará mais adiante, segue a solução por L'Hopital:
Seja
![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1}](/latexrender/pictures/576963920200cdc441033bc34d5a93e2.png)
. Substituindo x por 1 temos uma indeterminação do tipo

. Sendo assim, podemos usar a regra de L'Hopital que nada mais é do que derivar o numerador e derivar o denominador (separadamente) e posteriormente calcular o limite:
![\lim_{x\to 1}\frac{(\sqrt[m]{x} - 1)'}{(\sqrt[n]{x} - 1)'}=\lim_{x\to 1}\frac{\frac{1}{m}*x^{\frac{1-m}{m}}}{\frac{1}{n}*x^{\frac{1-n}{n}}}=\frac{\frac{1}{m}}{\frac{1}{n}}=\frac{n}{m} \lim_{x\to 1}\frac{(\sqrt[m]{x} - 1)'}{(\sqrt[n]{x} - 1)'}=\lim_{x\to 1}\frac{\frac{1}{m}*x^{\frac{1-m}{m}}}{\frac{1}{n}*x^{\frac{1-n}{n}}}=\frac{\frac{1}{m}}{\frac{1}{n}}=\frac{n}{m}](/latexrender/pictures/310cc61e1e78b2be8ed8d8ae85a6d2e1.png)

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por vdzz » Qua Fev 16, 2011 23:03
por vdzz » Qua Fev 16, 2011 23:03
Vou dar uma olhada em como se deriva, pois parece bem mais prático, valeu molina.
Esse seu segundo exemplo Luiz, achei mais tranquilo comparado ao primeiro.
Valeu pela ajuda (:
-
vdzz
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Fev 16, 2011 17:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. Elétrica
- Andamento: cursando
 por LuizAquino » Qui Fev 17, 2011 08:08
por LuizAquino » Qui Fev 17, 2011 08:08
vdzz escreveu:Esse seu segundo exemplo Luiz, achei mais tranquilo comparado ao primeiro.
Provavelmente você está dizendo isso pois no primeiro exemplo envolvia o trabalho com raízes. Gostaria de lhe deixar uma dica:
todo estudante da área de exatas é
obrigado a saber trabalhar com raízes (ou qualquer outro número que apareça)!
Se você não estiver lembrando das propriedades de radiciação, indico para você os vídeos do
Nerckie no YouTube:
Matemática Zero - Aula 10 - Radiciação - Primeira Parte (Total de 3 vídeos)
http://www.youtube.com/watch?v=K73GLTmT8YsMatemática Zero - Aula 12 - Racionalização - Primeira Parte (Total de 4 vídeos)
http://www.youtube.com/watch?v=qvVV_6mYVgo
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por LuizAquino » Sex Fev 18, 2011 10:19
por LuizAquino » Sex Fev 18, 2011 10:19
LuizAquino escreveu:Para aguçar ainda mais a curiosidade sobre esse exercício, poderíamos fazer ainda uma substituição bem elegante, que seria fazer
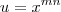
, pois desse modo o limite ficaria bem simples:
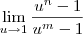
Apenas uma correção, a substituição é
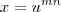
e não
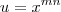
como foi escrito anteriormente.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] Gráfico e limite para função maior inteiro
 por Raphaela_sf » Qui Abr 05, 2012 19:26
por Raphaela_sf » Qui Abr 05, 2012 19:26
- 1 Respostas
- 6650 Exibições
- Última mensagem por LuizAquino

Qui Abr 05, 2012 20:53
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções reais de várias variáveis
por Bianca_R » Dom Nov 04, 2012 17:17
- 1 Respostas
- 4795 Exibições
- Última mensagem por MarceloFantini

Dom Nov 04, 2012 19:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5126 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] limite trigonométrico quando x tende ao infinito
por Ge_dutra » Seg Jan 28, 2013 10:13
- 2 Respostas
- 7270 Exibições
- Última mensagem por Ge_dutra

Ter Jan 29, 2013 14:20
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite de funções piso (maior inteiro)
por ViniciusAlmeida » Sáb Fev 14, 2015 10:09
- 2 Respostas
- 4446 Exibições
- Última mensagem por adauto martins

Qui Fev 19, 2015 15:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.










![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1}](/latexrender/pictures/576963920200cdc441033bc34d5a93e2.png)
![u = \sqrt[n]{x} u = \sqrt[n]{x}](/latexrender/pictures/e761d73d2c35c550efb26912c17251fc.png) , obtendo assim um novo limite (note que u também tenderá a 1):
, obtendo assim um novo limite (note que u também tenderá a 1):![\lim_{u\to 1}\frac{\sqrt[m]{u^n} - 1}{u - 1} \lim_{u\to 1}\frac{\sqrt[m]{u^n} - 1}{u - 1}](/latexrender/pictures/73a18bc8ba53226ac4b8dd6777ede4f6.png)
![\lim_{u\to 1}\frac{\left(\sqrt[m]{u}\right)^n - 1^n}{\left(\sqrt[m]{u}\right)^m - 1^m} \lim_{u\to 1}\frac{\left(\sqrt[m]{u}\right)^n - 1^n}{\left(\sqrt[m]{u}\right)^m - 1^m}](/latexrender/pictures/d68aa5ece324b8b9baa8ef25900e34e3.png)
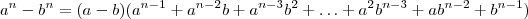 :
:![\lim_{u\to 1}\frac{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)}{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)} \lim_{u\to 1}\frac{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)}{(\sqrt[m]{u} - 1)(\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1)}](/latexrender/pictures/3f82820018e577a813531ec52cdb279d.png)
![\lim_{u\to 1}\frac{\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1}{\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1} \lim_{u\to 1}\frac{\sqrt[m]{u}^{n-1} + \sqrt[m]{u}^{n-2} + \sqrt[m]{u}^{n-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1}{\sqrt[m]{u}^{m-1} + \sqrt[m]{u}^{m-2} + \sqrt[m]{u}^{m-3}+\ldots \sqrt[m]{u}^2 + \sqrt[m]{u} + 1}](/latexrender/pictures/325e2d24ba59a30523c090e16a4666cc.png)
![\sqrt[m]{x}^k \sqrt[m]{x}^k](/latexrender/pictures/0e3cdc1b624d04beb3b97666dc34a824.png) (com k=n-1, n-2, ..., 1) no numerador será igual a 1. Quantos desses termos nós temos? Nós temos n-1 desses termos. Já no denominador nós temos m-1 termos do tipo
(com k=n-1, n-2, ..., 1) no numerador será igual a 1. Quantos desses termos nós temos? Nós temos n-1 desses termos. Já no denominador nós temos m-1 termos do tipo ![\sqrt[m]{x}^k \sqrt[m]{x}^k](/latexrender/pictures/0e3cdc1b624d04beb3b97666dc34a824.png) (com k=m-1, m-2, ..., 1).
(com k=m-1, m-2, ..., 1).![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} = \frac{(n-1)\cdot 1 + 1}{(m-1)\cdot 1 + 1} = \frac{n}{m} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} = \frac{(n-1)\cdot 1 + 1}{(m-1)\cdot 1 + 1} = \frac{n}{m}](/latexrender/pictures/2860d5a3ad57911cf300be5e313538d5.png)


![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1}](/latexrender/pictures/576963920200cdc441033bc34d5a93e2.png) . Substituindo x por 1 temos uma indeterminação do tipo
. Substituindo x por 1 temos uma indeterminação do tipo  . Sendo assim, podemos usar a regra de L'Hopital que nada mais é do que derivar o numerador e derivar o denominador (separadamente) e posteriormente calcular o limite:
. Sendo assim, podemos usar a regra de L'Hopital que nada mais é do que derivar o numerador e derivar o denominador (separadamente) e posteriormente calcular o limite:![\lim_{x\to 1}\frac{(\sqrt[m]{x} - 1)'}{(\sqrt[n]{x} - 1)'}=\lim_{x\to 1}\frac{\frac{1}{m}*x^{\frac{1-m}{m}}}{\frac{1}{n}*x^{\frac{1-n}{n}}}=\frac{\frac{1}{m}}{\frac{1}{n}}=\frac{n}{m} \lim_{x\to 1}\frac{(\sqrt[m]{x} - 1)'}{(\sqrt[n]{x} - 1)'}=\lim_{x\to 1}\frac{\frac{1}{m}*x^{\frac{1-m}{m}}}{\frac{1}{n}*x^{\frac{1-n}{n}}}=\frac{\frac{1}{m}}{\frac{1}{n}}=\frac{n}{m}](/latexrender/pictures/310cc61e1e78b2be8ed8d8ae85a6d2e1.png)


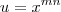 , pois desse modo o limite ficaria bem simples:
, pois desse modo o limite ficaria bem simples: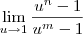

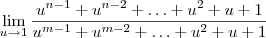
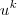 n-1 vezes no numerador e m-1 vezes no denominador, novamente o limite original é equivalente a:
n-1 vezes no numerador e m-1 vezes no denominador, novamente o limite original é equivalente a:![\lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} = \frac{(n-1)\cdot 1 + 1}{(m-1)\cdot 1 + 1} = \frac{n}{m} \lim_{x\to 1}\frac{\sqrt[m]{x} - 1}{\sqrt[n]{x} - 1} = \frac{(n-1)\cdot 1 + 1}{(m-1)\cdot 1 + 1} = \frac{n}{m}](/latexrender/pictures/2860d5a3ad57911cf300be5e313538d5.png)



, pois desse modo o limite ficaria bem simples:
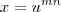 e não
e não 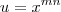 como foi escrito anteriormente.
como foi escrito anteriormente.





