 por alexandre32100 » Qua Nov 17, 2010 15:55
por alexandre32100 » Qua Nov 17, 2010 15:55
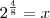
Esses tempos me deparei com o problema: "Qual o valor de
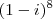
?". Não foi difícil chegar a solução
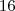
.
Mas, pensando de forma inversa, temos que
![\sqrt[8]{16}=\pm\sqrt{2} \sqrt[8]{16}=\pm\sqrt{2}](/latexrender/pictures/0365f73762c731a0a1247e06fc262fa2.png)
, porém, como foi visto,
![\sqrt[8]{16}=\pm(1-i) \sqrt[8]{16}=\pm(1-i)](/latexrender/pictures/dd6650408e55e1656804c69764788ed5.png)
, ou seja, a equação
![\sqrt[8]{16}=x \sqrt[8]{16}=x](/latexrender/pictures/2f5b91407574f13e93624dbbcc0a227e.png)
tem ao menos quatro soluções
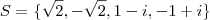
.
Queria saber qual o procedimento que devo adotar para encontrar, por exemplo, o resultado
![\sqrt[8]{16} \sqrt[8]{16}](/latexrender/pictures/38677f672db8178aef4615ff99faa1d9.png)
, tanto no conjunto dos números reais, quanto no dos números complexos.
-
alexandre32100
-
 por Molina » Qui Nov 18, 2010 14:51
por Molina » Qui Nov 18, 2010 14:51
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por victoreis1 » Qui Nov 18, 2010 15:15
por victoreis1 » Qui Nov 18, 2010 15:15
taí a fórmula de Moivre, para cálculo de raízes complexas:
![\sqrt[n] z = \sqrt[n]|z| [cos(\frac{\theta+2k\pi}{n}) + i sen (\frac{\theta+2k\pi}{n})] \sqrt[n] z = \sqrt[n]|z| [cos(\frac{\theta+2k\pi}{n}) + i sen (\frac{\theta+2k\pi}{n})]](/latexrender/pictures/6e4a80e4cc734b16f83d2d002afaad0f.png)
onde:
z é um número complexo;
k é um número natural positivo, que varia de 0 até n-1;
n é a raiz (no seu caso, raiz oitava, n = 8)
teta é o
argumento de z, ou seja, o ângulo, em radianos, que o segmento que liga o ponto no plano complexo que representa z e a origem forma com o eixo x.
note também que
![\sqrt[n]|z| \sqrt[n]|z|](/latexrender/pictures/3fa9a37672c4e91f0732141179ae9287.png)
é a raiz
real positiva do módulo, não complexa.
agora só substituir valores:
k = 0
![\sqrt[8] 16 = \sqrt[8]|16| [cos(\frac{0 + 0\pi}{8}) + i sen (\frac{0 + 0\pi}{8})] \sqrt[8] 16 = \sqrt[8]|16| [cos(\frac{0 + 0\pi}{8}) + i sen (\frac{0 + 0\pi}{8})]](/latexrender/pictures/48c27fc6d8a7943e302d8a8de4120bb8.png)
ficamos com:
![\sqrt[8] 16 = \sqrt[2] 2 (1 + 0) = \sqrt 2 \sqrt[8] 16 = \sqrt[2] 2 (1 + 0) = \sqrt 2](/latexrender/pictures/532faf7b195f17d7dad39a447f03d1fb.png)
Essa é a raiz para k = 0, haverão ainda outras sete raízes, para as quais k = 1, 2, 3, 4, 5, 6 e 7.
Tenta calcular usando esse mesmo método

-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por alexandre32100 » Qui Nov 18, 2010 16:42
por alexandre32100 » Qui Nov 18, 2010 16:42
molina escreveu: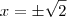
Sim, Molina, mas como mostrou o Victor, temos além destas, mais seis raizes complexas.
victoreis1 escreveu:taí a fórmula de Moivre, para cálculo de raízes complexas:
![\sqrt[n] z = \sqrt[n]|z| [cos(\frac{\theta+2k\pi}{n}) + i sen (\frac{\theta+2k\pi}{n})] \sqrt[n] z = \sqrt[n]|z| [cos(\frac{\theta+2k\pi}{n}) + i sen (\frac{\theta+2k\pi}{n})]](/latexrender/pictures/6e4a80e4cc734b16f83d2d002afaad0f.png)
onde:

é um número complexo;

é um número natural positivo, que varia de

até

;

é a raiz (no seu caso, raiz oitava,

)
teta é o argumento de

, ou seja, o ângulo, em radianos, que o segmento que liga o ponto no plano complexo que representa

e a origem forma com o eixo x.
Valeu cara, realmente esta fórmula é bastante útil neste, não a conhecia. Tinha criado um algoritmo para calcular as raizes complexas de um número e cheguei ao conjunto
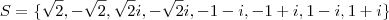
, mas creio que com a fórmula fica mais fácil.
-
alexandre32100
-
 por victoreis1 » Qui Nov 18, 2010 17:07
por victoreis1 » Qui Nov 18, 2010 17:07
isso.. note também que as raízes, dispostas no plano complexo, têm o mesmo módulo (raiz de 2) e formam um octágono regular..
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7466 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Limite - como resolver um lim quando temos raiz^2 e raiz^3.
por Monica santos » Sex Ago 16, 2013 14:22
- 4 Respostas
- 4154 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:01
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Como resolver raiz dentro de raiz ?
 por natyncb » Qui Abr 12, 2012 00:31
por natyncb » Qui Abr 12, 2012 00:31
- 10 Respostas
- 13809 Exibições
- Última mensagem por LuizAquino

Sex Ago 24, 2012 07:50
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo: limite com raiz dentro de raiz
 por roberto_trebor » Sáb Fev 15, 2014 20:45
por roberto_trebor » Sáb Fev 15, 2014 20:45
- 1 Respostas
- 2246 Exibições
- Última mensagem por Man Utd

Dom Fev 16, 2014 17:58
Cálculo: Limites, Derivadas e Integrais
-
- [Radiciação] Raiz dentro de raiz
por amandasousa_m » Sex Jul 19, 2013 09:37
- 2 Respostas
- 3445 Exibições
- Última mensagem por amandasousa_m

Sex Jul 19, 2013 21:58
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
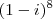 ?". Não foi difícil chegar a solução
?". Não foi difícil chegar a solução 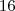 .
. ![\sqrt[8]{16}=\pm\sqrt{2} \sqrt[8]{16}=\pm\sqrt{2}](/latexrender/pictures/0365f73762c731a0a1247e06fc262fa2.png) , porém, como foi visto,
, porém, como foi visto, ![\sqrt[8]{16}=\pm(1-i) \sqrt[8]{16}=\pm(1-i)](/latexrender/pictures/dd6650408e55e1656804c69764788ed5.png) , ou seja, a equação
, ou seja, a equação ![\sqrt[8]{16}=x \sqrt[8]{16}=x](/latexrender/pictures/2f5b91407574f13e93624dbbcc0a227e.png) tem ao menos quatro soluções
tem ao menos quatro soluções 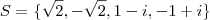 .
.![\sqrt[8]{16} \sqrt[8]{16}](/latexrender/pictures/38677f672db8178aef4615ff99faa1d9.png) , tanto no conjunto dos números reais, quanto no dos números complexos.
, tanto no conjunto dos números reais, quanto no dos números complexos.
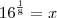
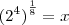

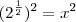
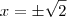


![\sqrt[n] z = \sqrt[n]|z| [cos(\frac{\theta+2k\pi}{n}) + i sen (\frac{\theta+2k\pi}{n})] \sqrt[n] z = \sqrt[n]|z| [cos(\frac{\theta+2k\pi}{n}) + i sen (\frac{\theta+2k\pi}{n})]](/latexrender/pictures/6e4a80e4cc734b16f83d2d002afaad0f.png)
![\sqrt[n]|z| \sqrt[n]|z|](/latexrender/pictures/3fa9a37672c4e91f0732141179ae9287.png) é a raiz
é a raiz ![\sqrt[8] 16 = \sqrt[8]|16| [cos(\frac{0 + 0\pi}{8}) + i sen (\frac{0 + 0\pi}{8})] \sqrt[8] 16 = \sqrt[8]|16| [cos(\frac{0 + 0\pi}{8}) + i sen (\frac{0 + 0\pi}{8})]](/latexrender/pictures/48c27fc6d8a7943e302d8a8de4120bb8.png)
![\sqrt[8] 16 = \sqrt[2] 2 (1 + 0) = \sqrt 2 \sqrt[8] 16 = \sqrt[2] 2 (1 + 0) = \sqrt 2](/latexrender/pictures/532faf7b195f17d7dad39a447f03d1fb.png)

 é um número complexo;
é um número complexo; é um número natural positivo, que varia de
é um número natural positivo, que varia de  até
até  ;
; é a raiz (no seu caso, raiz oitava,
é a raiz (no seu caso, raiz oitava,  )
)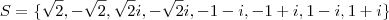 , mas creio que com a fórmula fica mais fácil.
, mas creio que com a fórmula fica mais fácil.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.