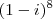 ?". Não foi difícil chegar a solução
?". Não foi difícil chegar a solução 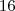 .
. Mas, pensando de forma inversa, temos que
![\sqrt[8]{16}=\pm\sqrt{2} \sqrt[8]{16}=\pm\sqrt{2}](/latexrender/pictures/0365f73762c731a0a1247e06fc262fa2.png) , porém, como foi visto,
, porém, como foi visto, ![\sqrt[8]{16}=\pm(1-i) \sqrt[8]{16}=\pm(1-i)](/latexrender/pictures/dd6650408e55e1656804c69764788ed5.png) , ou seja, a equação
, ou seja, a equação ![\sqrt[8]{16}=x \sqrt[8]{16}=x](/latexrender/pictures/2f5b91407574f13e93624dbbcc0a227e.png) tem ao menos quatro soluções
tem ao menos quatro soluções 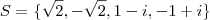 .
.Queria saber qual o procedimento que devo adotar para encontrar, por exemplo, o resultado
![\sqrt[8]{16} \sqrt[8]{16}](/latexrender/pictures/38677f672db8178aef4615ff99faa1d9.png) , tanto no conjunto dos números reais, quanto no dos números complexos.
, tanto no conjunto dos números reais, quanto no dos números complexos.
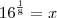
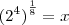
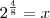

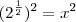
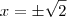


![\sqrt[n] z = \sqrt[n]|z| [cos(\frac{\theta+2k\pi}{n}) + i sen (\frac{\theta+2k\pi}{n})] \sqrt[n] z = \sqrt[n]|z| [cos(\frac{\theta+2k\pi}{n}) + i sen (\frac{\theta+2k\pi}{n})]](/latexrender/pictures/6e4a80e4cc734b16f83d2d002afaad0f.png)
![\sqrt[n]|z| \sqrt[n]|z|](/latexrender/pictures/3fa9a37672c4e91f0732141179ae9287.png) é a raiz
é a raiz ![\sqrt[8] 16 = \sqrt[8]|16| [cos(\frac{0 + 0\pi}{8}) + i sen (\frac{0 + 0\pi}{8})] \sqrt[8] 16 = \sqrt[8]|16| [cos(\frac{0 + 0\pi}{8}) + i sen (\frac{0 + 0\pi}{8})]](/latexrender/pictures/48c27fc6d8a7943e302d8a8de4120bb8.png)
![\sqrt[8] 16 = \sqrt[2] 2 (1 + 0) = \sqrt 2 \sqrt[8] 16 = \sqrt[2] 2 (1 + 0) = \sqrt 2](/latexrender/pictures/532faf7b195f17d7dad39a447f03d1fb.png)

 é um número complexo;
é um número complexo; é um número natural positivo, que varia de
é um número natural positivo, que varia de  até
até  ;
; é a raiz (no seu caso, raiz oitava,
é a raiz (no seu caso, raiz oitava,  )
)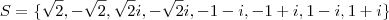 , mas creio que com a fórmula fica mais fácil.
, mas creio que com a fórmula fica mais fácil. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
