Gostaria de um auxílio nesta questão. Necessito saber se tem alguma coisa errada no seu desenvolvimento ou se a respota está correta. Agradeço.
CALCULE, CASO EXISTA, AS DERIVADAS PARCIAIS DA FUNÇÃO
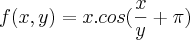 no ponto P(0,1)
no ponto P(0,1)DERIVADA EM FUNÇÃO DE X
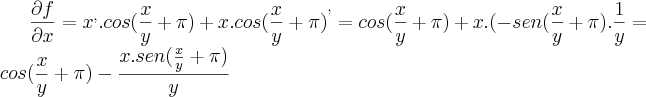
Substituindo pelos valores do ponto P(0,1), temos:
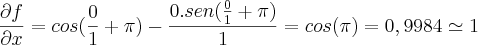
DERIVADA EM FUNÇÃO DE Y
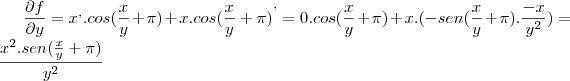
Substituindo pelos valores do ponto P(0,1), temos:
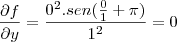
Sendo assim, a resposta é igual a P(1,0).



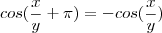
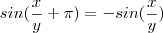
![\frac{\partial }{\partial x}\left[xcos(\frac{x}{y}+\pi))\right] =\frac{\partial }{\partial x}\left[-xcos(\frac{x}{y})\right] = x\frac{sin(\frac{x}{y})}{y} -cos{(\frac{y}{x})} =-x\frac{sin(\frac{x}{y}+\pi)}{y} +cos{(\frac{y}{x}+\pi)} \frac{\partial }{\partial x}\left[xcos(\frac{x}{y}+\pi))\right] =\frac{\partial }{\partial x}\left[-xcos(\frac{x}{y})\right] = x\frac{sin(\frac{x}{y})}{y} -cos{(\frac{y}{x})} =-x\frac{sin(\frac{x}{y}+\pi)}{y} +cos{(\frac{y}{x}+\pi)}](/latexrender/pictures/0b10457aaee27688093089d8457bd7f3.png)
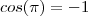 se for em radianos . Não entendi porque 0,9984 ....
se for em radianos . Não entendi porque 0,9984 ....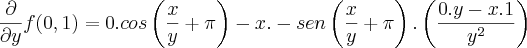
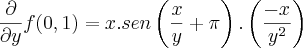
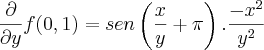
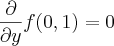

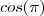 , ele me retornou esse resultado. Também fiquei sem saber, porque o site indicou -1 e não 0,9948, como na calculadora. Agora estou sem saber se o resultado é -1 ou 0,9948.
, ele me retornou esse resultado. Também fiquei sem saber, porque o site indicou -1 e não 0,9948, como na calculadora. Agora estou sem saber se o resultado é -1 ou 0,9948.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)