 por Fabio Cabral » Ter Mai 31, 2011 12:07
por Fabio Cabral » Ter Mai 31, 2011 12:07
Pessoal, estou com dúvida no seguinte limite:
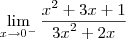
Em evidência, achei:
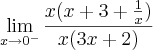
Daí não consigo mais.
Fiz vários cálculos, mas não consegui chegar em um resultado seguro.
Algúem aí?
Obrigado.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Fabio Cabral » Qua Jun 01, 2011 11:21
por Fabio Cabral » Qua Jun 01, 2011 11:21
Alguém?
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Fabio Cabral » Qua Jun 01, 2011 13:01
por Fabio Cabral » Qua Jun 01, 2011 13:01
Simples assim?
Com resultado: 1 . -

=
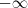
?
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Qua Jun 01, 2011 14:29
por LuizAquino » Qua Jun 01, 2011 14:29
Fabio Cabral escreveu:Simples assim?
Com resultado:
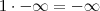
?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qua Jun 01, 2011 16:00
por Claudin » Qua Jun 01, 2011 16:00
Jogo de sinais normalmente Fábio!
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fabio Cabral » Qua Jun 01, 2011 18:47
por Fabio Cabral » Qua Jun 01, 2011 18:47
Veja,
Temos o seguinte limite calculado:
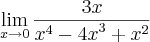
=
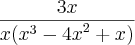
=
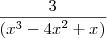
Usando a mesma teoria que você sugeriu:
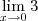
.
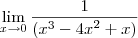
Logo, isso gerará o seguinte cálculo:
3 . 0 = 0
A pergunta é: O resultado é realmente 0 ? Isto esta correto?
É verdade que só posso usar evidênciar quando x tende a 0, - infinito e + infinito?
Grato
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Qua Jun 01, 2011 18:59
por LuizAquino » Qua Jun 01, 2011 18:59
A pergunta é: O resultado é realmente 0 ? Isto esta correto?
O valor do segundo limite não é zero.
Além disso, esse limite possui valores distintos quando analisamos pela esquerda e pela direita. Portanto, ele não existe.
É verdade que só posso usar evidenciar quando x tende a 0, - infinito e + infinito?
Não. Podemos usar essa técnica para x tendendo a outros valores.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Fabio Cabral » Qua Jun 01, 2011 19:20
por Fabio Cabral » Qua Jun 01, 2011 19:20
Compreendi.
Levando em conta esse limite :
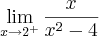 Não posso usar evidência por não ser 0, nem
Não posso usar evidência por não ser 0, nem  . Correto?
. Correto?Então, fiz da seguinte forma:
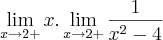
Agora sim, ficaria 2 .

=

Estou correto? Posso fazer dessa forma?
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Claudin » Qua Jun 01, 2011 19:38
por Claudin » Qua Jun 01, 2011 19:38
"Logo, isso gerará o seguinte cálculo:
3 . 0 = 0
A pergunta é: O resultado é realmente 0 ? Isto esta correto?"
O resultado do segundo limite seria
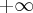
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Claudin » Qua Jun 01, 2011 19:40
por Claudin » Qua Jun 01, 2011 19:40
Fabio Cabral escreveu:Compreendi.
Levando em conta esse limite :
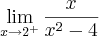 Não posso usar evidência por não ser 0, nem
Não posso usar evidência por não ser 0, nem  . Correto?
. Correto?Então, fiz da seguinte forma:
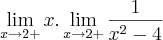
Agora sim, ficaria 2 .

=

Estou correto? Posso fazer dessa forma?
Sim.

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fabio Cabral » Qua Jun 01, 2011 20:14
por Fabio Cabral » Qua Jun 01, 2011 20:14
Ceerto !
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por LuizAquino » Qui Jun 02, 2011 15:11
por LuizAquino » Qui Jun 02, 2011 15:11
Claudin escreveu:"Logo, isso gerará o seguinte cálculo:
3 . 0 = 0
A pergunta é: O resultado é realmente 0 ? Isto esta correto?"
O resultado do segundo limite seria
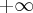
Errado. Como eu falei antes, temos que
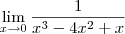
não existe, pois os laterais são distintos. Ou seja, temos que:
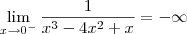
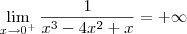
Fabio Cabral escreveu: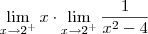
Agora sim, ficaria
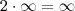
Estou correto? Posso fazer dessa forma?
Está errado, pois você não especificou se é mais infinito ou menos infinito. Nesse caso, o valor do limite será menos infinito.
Editado pela última vez por
LuizAquino em Qui Jun 02, 2011 16:48, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qui Jun 02, 2011 16:01
por Claudin » Qui Jun 02, 2011 16:01
No caso do

analisei a operação e achei que era 2 vezes mais infinito por isso falei que estava certo!
E sobre o segundo limite esta errado msm, me equivoquei com os laterais.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fabio Cabral » Qui Jun 02, 2011 16:37
por Fabio Cabral » Qui Jun 02, 2011 16:37
Fabio Cabral escreveu: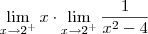
Agora sim, ficaria
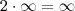
Estou correto? Posso fazer dessa forma?
Está errado, pois você não especificou se é mais infinito ou menos infinito. Nesse caso, será menos infinito.[/quote]
Pensei que

fosse a mesma coisa que
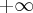
.
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
 por Claudin » Qui Jun 02, 2011 16:40
por Claudin » Qui Jun 02, 2011 16:40
Eu imaginei também que você tinha pensado nisso
por isso falei que estava correto, mas na próxima especifica os sinais entao.
Abraço
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fabio Cabral » Qui Jun 02, 2011 16:41
por Fabio Cabral » Qui Jun 02, 2011 16:41
Bom, a partir de agora, passemos a apresentar o sinal sempre !
" A Matemática não mente. Mente quem faz mau uso dela. " - Albert Einstein
-
Fabio Cabral
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Qua Out 06, 2010 11:33
- Localização: Brasília-DF
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Simplificação de Limites] - Produtos notáveis
por nick_arcos » Qui Set 20, 2012 17:39
- 2 Respostas
- 3403 Exibições
- Última mensagem por Thyago Quimica

Sáb Set 22, 2012 15:32
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Simplificação algébrica para determinar limites
por Reh » Qua Fev 28, 2018 02:41
- 4 Respostas
- 8485 Exibições
- Última mensagem por DarioCViveiros

Qui Mar 01, 2018 23:50
Cálculo: Limites, Derivadas e Integrais
-
- Simplificação - Ajuda Dúvidas em relação a simplificação
por wgf » Qui Mai 16, 2013 12:56
- 1 Respostas
- 2249 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 18:03
Equações
-
- [Simplificação]Fazer a simplificação da resposta
por neoreload » Qua Fev 04, 2015 05:50
- 3 Respostas
- 2709 Exibições
- Última mensagem por neoreload

Sáb Fev 07, 2015 22:10
Equações
-
- [SIMPLIFICAÇÃO] Simplificação expoentes
por brunnkpol » Ter Mai 07, 2013 17:00
- 1 Respostas
- 1730 Exibições
- Última mensagem por DanielFerreira

Sex Mai 10, 2013 00:40
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
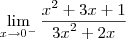
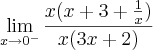

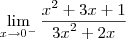
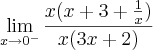


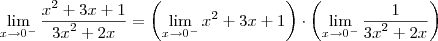

 =
= 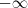 ?
?
?


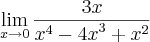
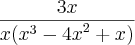
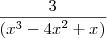
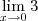 .
. 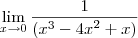


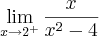
 . Correto?
. Correto?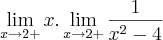
 =
= 

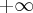

. Correto?
=



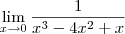 não existe, pois os laterais são distintos. Ou seja, temos que:
não existe, pois os laterais são distintos. Ou seja, temos que: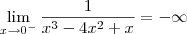
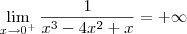



 fosse a mesma coisa que
fosse a mesma coisa que 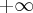 .
.







