 por john » Dom Fev 13, 2011 16:19
por john » Dom Fev 13, 2011 16:19
Olá pessoal!
Estou com dúvidas nas seguintes integrais:
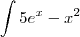
Não vejo forma de integrar
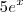
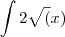
Não vejo forma de integrar
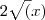
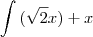
O x eu sei integrar. Não sei é a outra parte da expressão.
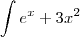
Não consegui de todo integrar o
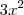
Preciso mesmo de ajuda, visto que tenho exame para a semana e estou mesmo confuso nesta matéria. Obrigado pela atenção!
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Dom Fev 13, 2011 16:35
por Neperiano » Dom Fev 13, 2011 16:35
Ola
Peço desculpa que não sei usar o latex
Vou resolver uma delas, a mais dificil e dar dicas para resolver as outras
Integral de (raiz de 2x) + x
Integral de raiz de 2x = (2x)^1/2 + x
Como é soma divida em duas integrais
integral de (2x)^1/2 + Integral de x
u = 2x
du = 2
Logo integral de (u^1/2).1/2
Passe o 1/2 pra frente
1/2 Integral de u^1/2
1/2 + 1 = 3/2
1/2.(u^3/2)/3/2
1/3.(2x)^3/2 + (x^2)/2
Algumas dicas
1- Sempre que for adição ou subtração divida em duas integrais
2- Quando tiver numero passe ele pra fora da integral
3 - Procure sempre o U quando houver uma função dentro da outra f(g(x))
4 - raix de x = x^/2
Espero ter ajudado
Qualquer duvida
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por john » Dom Fev 13, 2011 16:44
por john » Dom Fev 13, 2011 16:44
Obrigado pela pronta resposta e pelas dicas.
Contudo eu não percebi esta parte:
Logo integral de (u^1/2).1/2
Passe o 1/2 pra frente
1/2 Integral de u^1/2
Poderia-me ajudar?
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Dom Fev 13, 2011 16:48
por Neperiano » Dom Fev 13, 2011 16:48
Ola
Claro claro
Quando voce tem um numero voce passa ele pra fora da integral e depois multiplique ele
Ex:
Integral de 5x^2
5 Integral de x^2
5.(x^3)/3
(5x^3)/3
Entendeu?
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por john » Dom Fev 13, 2011 16:59
por john » Dom Fev 13, 2011 16:59
Mais uma vez obrigado. Nesse exemplo eu percebi. Mas o outro está me a fazer alguma confusão. Como a derivada de u é 2 não deveríamos colocar um 2 antes do 2x e 1/2 fora para compensar?
Obrigado!
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Dom Fev 13, 2011 17:54
por Neperiano » Dom Fev 13, 2011 17:54
Ola
Hehehhe a derivada de 2x = 2, na verdade eu so substitui por u pra facilita
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por john » Dom Fev 13, 2011 19:16
por john » Dom Fev 13, 2011 19:16
E o 1/3 do fim vem de onde? Estou confuso.
Obrigado.
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Neperiano » Dom Fev 13, 2011 19:32
por Neperiano » Dom Fev 13, 2011 19:32
Ola
1/2.(u^3/2)/3/2
Passei ele pra cima ao inverso
1/2.(u^3/2).2/3
Dai eu multiplico e fica 2/6 = 1/3
Espero ter ajudado
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por john » Dom Fev 13, 2011 20:27
por john » Dom Fev 13, 2011 20:27
Ah ok. Já percebi. Muito obrigado.
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [integrais] Calculando áreas - Integrais
 por Faby » Seg Set 19, 2011 10:55
por Faby » Seg Set 19, 2011 10:55
- 11 Respostas
- 8867 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 18:03
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por pseytow » Qui Nov 27, 2008 21:54
- 1 Respostas
- 2819 Exibições
- Última mensagem por Adriano Tavares

Qui Mar 10, 2011 01:52
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por panneitz » Dom Jun 07, 2009 19:55
- 1 Respostas
- 2448 Exibições
- Última mensagem por Marcampucio

Dom Jun 07, 2009 20:31
Cálculo: Limites, Derivadas e Integrais
-
- Integrais
por leha » Ter Nov 10, 2009 16:08
- 2 Respostas
- 2534 Exibições
- Última mensagem por leha

Sex Nov 13, 2009 08:56
Cálculo: Limites, Derivadas e Integrais
-
- Integrais em IR3
por Saruman » Sáb Mai 22, 2010 10:27
- 1 Respostas
- 2143 Exibições
- Última mensagem por luispereira

Ter Dez 28, 2010 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
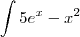
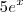
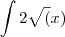
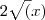
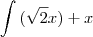
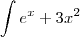
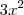



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
