 por fernandocez » Dom Mar 06, 2011 12:12
por fernandocez » Dom Mar 06, 2011 12:12
48. O raio da circunferência que tem centro no ponto (3,4) e tangencia e reta da equação x+2y = 1 é:
resp.:
![2\sqrt[]{5} 2\sqrt[]{5}](/latexrender/pictures/8afe59aad7560ad383eefaf7fd49cdb9.png)
Essa eu consegui fazer mas estou com dúvida se usei o caminho certo ou mais curto.
Eu fiz assim:
Encotrei a distância entre o centro da circunferência P(3,4) e a reta (x+2y = 1). Prá isso usei essa fórmula.
d(P,r) =
![\frac{\left|ax+by+c \right|}{\sqrt[]{{a}^{2}+{b}^{2}}} \frac{\left|ax+by+c \right|}{\sqrt[]{{a}^{2}+{b}^{2}}}](/latexrender/pictures/0932dfd3e31795311f9b2ae064b66444.png)
=
![\frac{\left|-\frac{1}{2}3-1*4+\frac{1}{2} \right|}{\sqrt[]{{\left(-\frac{1}{2} \right)}^{2}+{\left(-1 \right)}^{2}}} \frac{\left|-\frac{1}{2}3-1*4+\frac{1}{2} \right|}{\sqrt[]{{\left(-\frac{1}{2} \right)}^{2}+{\left(-1 \right)}^{2}}}](/latexrender/pictures/924e8b03aaa4668a34765f00bc28a9be.png)
=
![2\sqrt[]{5} 2\sqrt[]{5}](/latexrender/pictures/8afe59aad7560ad383eefaf7fd49cdb9.png)
Eu queria saber se o caminho tá bom ou teria um mais rápido no concurso?
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por Renato_RJ » Dom Mar 06, 2011 15:13
por Renato_RJ » Dom Mar 06, 2011 15:13
Fernando, eu acho esse método o mais rápido mesmo, pois você usou a fórmula para achar a distância entre um ponto e uma reta dada sua equação geral, mas achei suas contas confusas, eu fiz desse jeito, veja:
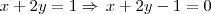
Agora que eu tenho a equação da reta na forma ax + by + c =0, posso usar a fórmula:

Retirando a raiz do denominador, teremos:
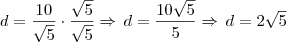
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por fernandocez » Dom Mar 06, 2011 17:30
por fernandocez » Dom Mar 06, 2011 17:30
Renato_RJ escreveu:Fernando, eu acho esse método o mais rápido mesmo, pois você usou a fórmula para achar a distância entre um ponto e uma reta dada sua equação geral, mas achei suas contas confusas...
Valeu Renato, ficou muito mais fácil. Realmente o que eu fiz fica muito trabalhoso. É que peguei a equação: x+2y = 1 e ignorantemente arrumei ela até ficar: -x/2-y+1/2=0 e não tinha necessidade, era só pegar a eq. x+2y = 1 e igualar a 0: x+2y-1 = 0 que nem vc fez. Obrigado.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 19:10
- 6 Respostas
- 3567 Exibições
- Última mensagem por fernandocez

Sáb Fev 26, 2011 22:29
Geometria Plana
-
- Questão prova concurso
por fernandocez » Sáb Fev 26, 2011 23:27
- 3 Respostas
- 2507 Exibições
- Última mensagem por fernandocez

Dom Fev 27, 2011 10:33
Funções
-
- Questão prova concurso (sen e cos)
por fernandocez » Qua Mar 02, 2011 11:26
- 13 Respostas
- 9301 Exibições
- Última mensagem por fernandocez

Dom Mar 13, 2011 12:18
Trigonometria
-
- Questão prova concurso com Latitude
por fernandocez » Sáb Fev 26, 2011 23:38
- 2 Respostas
- 1827 Exibições
- Última mensagem por fernandocez

Qua Mar 02, 2011 11:27
Geometria Plana
-
- Questão prova concurso combinatória
por fernandocez » Ter Mar 01, 2011 12:35
- 2 Respostas
- 2680 Exibições
- Última mensagem por fernandocez

Qui Mar 03, 2011 22:47
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![2\sqrt[]{5} 2\sqrt[]{5}](/latexrender/pictures/8afe59aad7560ad383eefaf7fd49cdb9.png)
![\frac{\left|ax+by+c \right|}{\sqrt[]{{a}^{2}+{b}^{2}}} \frac{\left|ax+by+c \right|}{\sqrt[]{{a}^{2}+{b}^{2}}}](/latexrender/pictures/0932dfd3e31795311f9b2ae064b66444.png) =
= ![\frac{\left|-\frac{1}{2}3-1*4+\frac{1}{2} \right|}{\sqrt[]{{\left(-\frac{1}{2} \right)}^{2}+{\left(-1 \right)}^{2}}} \frac{\left|-\frac{1}{2}3-1*4+\frac{1}{2} \right|}{\sqrt[]{{\left(-\frac{1}{2} \right)}^{2}+{\left(-1 \right)}^{2}}}](/latexrender/pictures/924e8b03aaa4668a34765f00bc28a9be.png) =
= ![2\sqrt[]{5} 2\sqrt[]{5}](/latexrender/pictures/8afe59aad7560ad383eefaf7fd49cdb9.png)


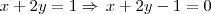

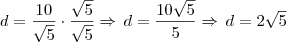
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
