 por DanielRJ » Ter Ago 24, 2010 13:07
por DanielRJ » Ter Ago 24, 2010 13:07
Olá pessoal tenho duvidas sobre exercicios meu objetivo é sanar todas essas duvidas mas é somente uma por topico então vamos devagar!
(AFA) A quantidade de numeros naturais de 4 algarismos distintos que podem ser formados por 1.2.3.4.5 e 6, que contém o algarismo 3 ou 4 é?
a)196
b)286
c)336
d)446
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por alexandre32100 » Ter Ago 24, 2010 15:24
por alexandre32100 » Ter Ago 24, 2010 15:24
Pra começar você deve definir a quantidade de números de quatro algarismos distintos com os números
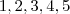
e

, sem se importar se há ou não um

ou

entre eles, que é

(

escolhas possíveis para o primeiro algarismo,
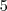
escolhas para o segundo,

para o terceiro e

para o quarto).
Depois, deve excluir deste total os números que não possuem nem o

, nem o

. Estes número são formados apenas pelos algarismo
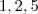
e

, totalizando
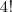
possibilidades.
Concluindo,
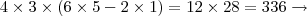 alternativa c
alternativa c.
-
alexandre32100
-
 por DanielRJ » Ter Ago 24, 2010 15:42
por DanielRJ » Ter Ago 24, 2010 15:42
Obrigado alexandre cheguei a esboçar isso mas pensei errado valeu!
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (( Analise combinatória ))
por Roberta » Dom Jul 13, 2008 17:28
- 8 Respostas
- 16390 Exibições
- Última mensagem por Aparecida

Sáb Mai 05, 2012 00:07
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:20
- 4 Respostas
- 12560 Exibições
- Última mensagem por Neilson

Ter Mai 01, 2012 01:23
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Sex Set 12, 2008 23:26
- 2 Respostas
- 8482 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 15, 2008 10:08
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:52
- 3 Respostas
- 7935 Exibições
- Última mensagem por Rejane Sampaio

Qui Set 25, 2008 10:43
Estatística
-
- Análise Combinatória
por Rejane Sampaio » Qua Set 17, 2008 15:56
- 2 Respostas
- 6630 Exibições
- Última mensagem por Rejane Sampaio

Seg Set 22, 2008 11:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


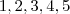 e
e  , sem se importar se há ou não um
, sem se importar se há ou não um  ou
ou  entre eles, que é
entre eles, que é  (
(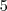 escolhas para o segundo,
escolhas para o segundo, 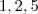 e
e 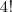 possibilidades.
possibilidades.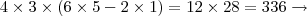

 .
.



