Considere uma prova de matemática constituída de 4 questões de múltiplas escolha, com cada alternativa cada uma, das quais apenas uma é correta. Um candidato resolve fazer essa prova escolhendo aleatóriamente uma alternativa em cada questão. Então é correto afirmar que a probabilidade de esse candidato acertar, nessa prova, exatamente 1 questão é:
a) 27/64 b) 27/256 c) 9/64 d) 9/256
A minha resolução - no que foi que eu errei e porque?
1 . temos 1/4 de possibilidade de acertar em cada questão
2 . são situações independentes sendo que o fato de haver 1/4 de chances de ele acertar em cada questão e o fato e ele acertar somente 1 das questões
não deveria ser um caso de multiplicação das probabilidades? tipo 1/4 de chances de acertar em cada questão X 1/4 de chances de acertar somente 1 questão?


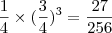

 , logo a probabilidade de errar é de
, logo a probabilidade de errar é de  , pois
, pois 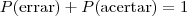 . Assim, ele pode
. Assim, ele pode 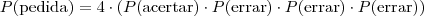
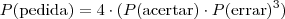
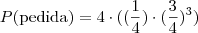
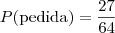



 .
.
 :
: