 por Fernanda Lauton » Seg Abr 19, 2010 15:55
por Fernanda Lauton » Seg Abr 19, 2010 15:55
Considere uma prova de matemática constituída de 4 questões de múltiplas escolha, com cada alternativa cada uma, das quais apenas uma é correta. Um candidato resolve fazer essa prova escolhendo aleatóriamente uma alternativa em cada questão. Então é correto afirmar que a probabilidade de esse candidato acertar, nessa prova, exatamente 1 questão é:
a) 27/64 b) 27/256 c) 9/64 d) 9/256
A minha resolução - no que foi que eu errei e porque?
1 . temos 1/4 de possibilidade de acertar em cada questão
2 . são situações independentes sendo que o fato de haver 1/4 de chances de ele acertar em cada questão e o fato e ele acertar somente 1 das questões
não deveria ser um caso de multiplicação das probabilidades? tipo 1/4 de chances de acertar em cada questão X 1/4 de chances de acertar somente 1 questão?
Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por davi_11 » Seg Abr 19, 2010 16:21
por davi_11 » Seg Abr 19, 2010 16:21
minha resolução:
possibilidades dele acertar uma questão X possibilidades dele errar as outras 3
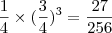
"Se é proibido pisar na grama, o jeito é deitar e rolar..."
-
davi_11
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 02, 2010 22:47
- Localização: Leme - SP
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em eletrotécnica
- Andamento: formado
 por Fernanda Lauton » Seg Abr 19, 2010 16:42
por Fernanda Lauton » Seg Abr 19, 2010 16:42
Naum entendi


Fernanda lauton
-
Fernanda Lauton
- Usuário Parceiro

-
- Mensagens: 58
- Registrado em: Seg Mar 29, 2010 17:21
- Localização: Minas Gerais
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Biologia
- Andamento: formado
 por MarceloFantini » Seg Abr 19, 2010 19:49
por MarceloFantini » Seg Abr 19, 2010 19:49
Eu faria assim:
A probabilidade de acertar uma questão é de

, logo a probabilidade de errar é de

, pois
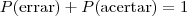
. Assim, ele pode
acertar a primeira e errar a segunda e errar a terceira e errar a quarta. Note que o
e é o princípio multiplicativo. Porém, ele não precisa
necessariamente acertar a primeira e errar as outras. Pode ser que ele acerte a quarta, ou a terceira, e erre as outras. Portanto:
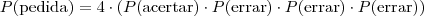
O quatro multiplicando quer dizer o número de possibilidades de troca de ordem.
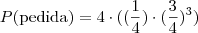
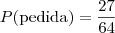
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Probabilidade] Exercício Desafio de Probabilidade
por werwer » Qua Mar 21, 2012 18:57
- 0 Respostas
- 10349 Exibições
- Última mensagem por werwer

Qua Mar 21, 2012 18:57
Estatística
-
- Probabilidade - Função Densidade de Probabilidade
por pimgui » Qua Dez 16, 2020 10:53
- 0 Respostas
- 21660 Exibições
- Última mensagem por pimgui

Qua Dez 16, 2020 10:53
Probabilidade
-
- Probabilidade - função probabilidade
por tarlix » Ter Mai 24, 2011 12:41
- 1 Respostas
- 5349 Exibições
- Última mensagem por Neperiano

Dom Out 16, 2011 17:00
Estatística
-
- [Probabilidade] probabilidade de obj com estudantes
por fenixxx » Seg Ago 13, 2012 14:06
- 1 Respostas
- 4525 Exibições
- Última mensagem por Neperiano

Ter Out 09, 2012 10:10
Probabilidade
-
- [probabilidade condicional] probabilidade de gol.
 por Mr_ MasterMind » Sáb Set 19, 2015 17:35
por Mr_ MasterMind » Sáb Set 19, 2015 17:35
- 0 Respostas
- 4536 Exibições
- Última mensagem por Mr_ MasterMind

Sáb Set 19, 2015 17:35
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


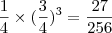

 , logo a probabilidade de errar é de
, logo a probabilidade de errar é de  , pois
, pois 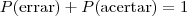 . Assim, ele pode
. Assim, ele pode 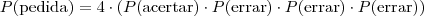
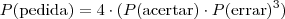
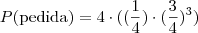
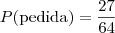




 , avisa que eu resolvo.
, avisa que eu resolvo.

