A distribuição é a seguinte:
Caixa A:
Bolas amarelas: 5
Bolas verdes: 5
Caixa B:
Bolas amarelas: 2
Bolas verdes: 8
Caixa C:
Bolas amarelas: 6
Bolas verdes: 4
Escolhendo aleatoriamente uma caixa, qual é a probabilidade de tirar uma bola verde?
Se fosse uma probabilidade condicional, do tipo, qual a probabilidade de tirar bola verde sabendo que se tirou da caixa A, seria facil.Pois os casos favoraveis limitavam-se às bolas verdes que estão na caixa A.
Se eu fizer 3 probabilidades condicionadas, cada uma relativa a tirar uma bola de cada uma das caixas, então basta somar as 3 probabilidades condicionadas.Mas isto é a mesma coisa se as 30 bolas estivessem numa unica caixa.Logo:

Será assim?


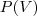
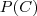
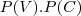 , ou seja,
, ou seja, 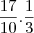
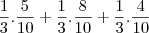 , que é basicamente o que foi dito em
, que é basicamente o que foi dito em 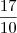 , mas probabilidade, por definição é um número entre 0 e 1.
, mas probabilidade, por definição é um número entre 0 e 1.

 .
.
 :
: