Resolvi a seguinte inequação:
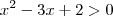 e obtive os dois resultados:
e obtive os dois resultados:x1 = 2
x2 = 1
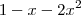 , essa com:
, essa com:x1 = -1
x2 =
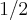
Mas não compreendo o que isso significa! Como fica esses intervalos na reta dos reais ?
Valeu!

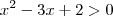 e obtive os dois resultados:
e obtive os dois resultados: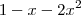 , essa com:
, essa com: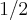






 (se for positivo a concavidade da parábola é para cima e se for negativo a concavidade é para baixo). A partir disso você só precisa calcular as raízes e imaginar essa parábola cortando o eixo x nessas raízes. Lembrando que algumas parábolas não cortam o eixo x.
(se for positivo a concavidade da parábola é para cima e se for negativo a concavidade é para baixo). A partir disso você só precisa calcular as raízes e imaginar essa parábola cortando o eixo x nessas raízes. Lembrando que algumas parábolas não cortam o eixo x.
Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: