Bom dia.
Não consegui resolver essa questão, podem me ajudar por favor?
Dados f(g(x)) = x e g(x) = 2x-1, determine f(x)?
f(2x-1) = x mas não sei o que devo fazer depois porque foi dado g(x). Se fosse f(x) eu saberia continuar.
Agradeço a ajuda.





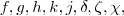 e etc. são só nomes sugestivos para a função .Aquelas dicas se adapta-a este caso . Se novamente não conseguir prosseguir ,post .
e etc. são só nomes sugestivos para a função .Aquelas dicas se adapta-a este caso . Se novamente não conseguir prosseguir ,post .

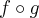 ( e não
( e não  ) e
) e 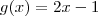 .
.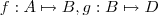 (com
(com 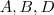 não vazios ). Admita
não vazios ). Admita  sobrejetiva , então
sobrejetiva , então  admite inversa à direita . Seja
admite inversa à direita . Seja  inversa de
inversa de  à direita .Pela hipótese
à direita .Pela hipótese 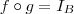 ,onde
,onde 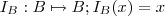 é a função identidade .Além disso , se
é a função identidade .Além disso , se  for também injetora e
for também injetora e  for inversa à esquerda de
for inversa à esquerda de  (ou seja,
(ou seja, 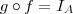 ) ,então dizemos que
) ,então dizemos que  é invertível e
é invertível e  é sua inversa .
é sua inversa .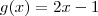 e
e  e queremos determinar
e queremos determinar  .Ora ,pela teoria acima
.Ora ,pela teoria acima  é sobrejetora e
é sobrejetora e  sua inversa à direita . Agora se considerarmos
sua inversa à direita . Agora se considerarmos  injetora e
injetora e  sua inversa à esquerda ,chegaríamos a conclusão que
sua inversa à esquerda ,chegaríamos a conclusão que 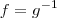 que é a função inversa de
que é a função inversa de  . Agora basta determinar
. Agora basta determinar 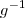 .
.
santhiago escreveu:Você tem razão ,agora que notei ,o que temos é( e não
) e
.
Observação .
Considere as funções(com
não vazios ). Admita
sobrejetiva , então
admite inversa à direita . Seja
inversa de
à direita .Pela hipótese
,onde
é a função identidade .Além disso , se
for também injetora e
for inversa à esquerda de
(ou seja,
) ,então dizemos que
é invertível e
é sua inversa .
Em relação ao exercício , foi dadoe
e queremos determinar
.Ora ,pela teoria acima
é sobrejetora e
sua inversa à direita . Agora se considerarmos
injetora e
sua inversa à esquerda ,chegaríamos a conclusão que
que é a função inversa de
. Agora basta determinar
.

Lana Brasil escreveu:santhiago escreveu:Você tem razão ,agora que notei ,o que temos é( e não
) e
.
Observação .
Considere as funções(com
não vazios ). Admita
sobrejetiva , então
admite inversa à direita . Seja
inversa de
à direita .Pela hipótese
,onde
é a função identidade .Além disso , se
for também injetora e
for inversa à esquerda de
(ou seja,
) ,então dizemos que
é invertível e
é sua inversa .
Em relação ao exercício , foi dadoe
e queremos determinar
.Ora ,pela teoria acima
é sobrejetora e
sua inversa à direita . Agora se considerarmos
injetora e
sua inversa à esquerda ,chegaríamos a conclusão que
que é a função inversa de
. Agora basta determinar
.
Obrigada pela sua boa vontade. A explicação teórica está difícil de entender para o pouco que sei de função, por enquanto. Mesmo assim muito obrigada. O que fiz foi isso: g(x)^-1 = (x+1)/2 então g((x+1)/2) = x e f(g(x)) = x então f(x) = (x+1)/2. Está correto??

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante