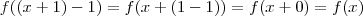por 13run0 » Qui Mai 27, 2010 17:54
por 13run0 » Qui Mai 27, 2010 17:54
Se f(x+1)=
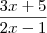
, (x

-

), então o domínio da função f(x) é o conjunto formado pelos números reais
x tais que:
Resposta: x


ele dá a função f(x+1). . . mas como eu encontro a função f(x) ??
-
13run0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Mai 27, 2010 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Edificações
- Andamento: formado
 por Neperiano » Qui Mai 27, 2010 18:35
por Neperiano » Qui Mai 27, 2010 18:35
Ola
Substitua o x por -1/2 depois de resolvido, diminua 1
Acredito ser isso
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por 13run0 » Qui Mai 27, 2010 23:54
por 13run0 » Qui Mai 27, 2010 23:54
Maligno, valeu por tentar me ajudar. . .
mas eu não consegui resolver a questão. . .
se vcou outra pessoa puder mostrar a resolução eu agradeço. . .
-
13run0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Mai 27, 2010 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Edificações
- Andamento: formado
 por Molina » Sex Mai 28, 2010 01:25
por Molina » Sex Mai 28, 2010 01:25
Boa noite.
Como
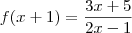
temos que:
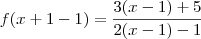
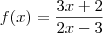
Agora você tem

. O que eu fiz foi subtrair 1 de x, para chegar em
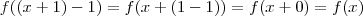
Como subtrai 1 no argumento, subtrai 1 também na lei de formação, e chegamos nesta resposta a cima.
Agora é só fazer o denominador diferente de 0 e achar a resposta de x.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por 13run0 » Sex Mai 28, 2010 14:15
por 13run0 » Sex Mai 28, 2010 14:15
Valeu mesmo Molina!
ótima explicação. . .
me ajudou bastante!!
-
13run0
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Mai 27, 2010 15:48
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Edificações
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função Quadrática MACK
por Julio_Cesar » Qua Jul 13, 2011 14:18
- 1 Respostas
- 1179 Exibições
- Última mensagem por LuizAquino

Seg Jul 25, 2011 15:52
Funções
-
- (MACK) Em [0, 2?], se...
por manuoliveira » Ter Jun 01, 2010 21:02
- 2 Respostas
- 2685 Exibições
- Última mensagem por Mathmatematica

Dom Jun 06, 2010 21:22
Binômio de Newton
-
- Mack-SP
por -Sarah- » Sáb Fev 23, 2013 18:56
- 4 Respostas
- 2946 Exibições
- Última mensagem por -Sarah-

Ter Fev 26, 2013 20:20
Funções
-
- mack
 por fna » Qua Jun 12, 2013 08:53
por fna » Qua Jun 12, 2013 08:53
- 0 Respostas
- 940 Exibições
- Última mensagem por fna

Qua Jun 12, 2013 08:53
Geometria Plana
-
- (Mack 98) Circunferência
 por rafaelcb » Qui Set 30, 2010 13:05
por rafaelcb » Qui Set 30, 2010 13:05
- 2 Respostas
- 4786 Exibições
- Última mensagem por rafaelcb

Sex Out 01, 2010 03:17
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
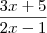 , (x
, (x -
- ), então o domínio da função f(x) é o conjunto formado pelos números reais x tais que:
), então o domínio da função f(x) é o conjunto formado pelos números reais x tais que:


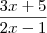 , (x
, (x -
- ), então o domínio da função f(x) é o conjunto formado pelos números reais x tais que:
), então o domínio da função f(x) é o conjunto formado pelos números reais x tais que:




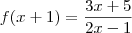 temos que:
temos que: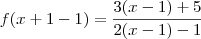
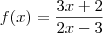
 . O que eu fiz foi subtrair 1 de x, para chegar em
. O que eu fiz foi subtrair 1 de x, para chegar em