 por viduani » Qui Ago 02, 2012 14:43
por viduani » Qui Ago 02, 2012 14:43
Boa tarde! Não sei se estou entendendo errado a idéia de imagem, mas, tentei fazer uma função modular do tipo:
I 3x - 1 I - 5, definida em R cujo valor de f é (1/3) e (-1/3). Eu encontrei os valores -5 e -3. O problema passou a surgir quando ele me perguntou o conjunto imagem dessa função. Pelo que eu entendo de conjunto imagem significa o reflexo dos valores que você atribui a X substituindo na equação tais valores e encontra o seu resultado. Nessa questão eu usei valores imaginários de -2,-1,0,1,2 e pensei que seus resultados na equação fossem a sua imagem. O livro diz que o conjunto imagem dessa questão é {y E R/y>ou igual a 5}. Ele admite valores maiores ou iguais a 5 e somente 5, por que?
-
viduani
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sex Jul 13, 2012 20:03
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: curso m3
- Andamento: cursando
 por e8group » Qui Ago 02, 2012 17:02
por e8group » Qui Ago 02, 2012 17:02
Boa tarde, você estar certo que a função modular trata-se de
|3x-1| - 5 ? Se sua resposta for sim o gabarito não faz sentido ,entretanto se sua função modular na verdade é da forma |3x-1| +5 perceba que realmente
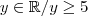
isto é a imagem da função modular é maior ou igual a 5 para domínio real ,em outras palavras ,
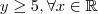
Obs.: Sua "visão "sobre o conceito de imagem estar correto .Imagem é ,para todo elemento no contradomínio existe pelo menos um associado a
um ou mais elementos no domínio .Há casos que diferentes valores no domínio estar associado a um mesmo elemento no CD .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sex Ago 03, 2012 03:20
por MarceloFantini » Sex Ago 03, 2012 03:20
santhiago escreveu:Obs.: Sua "visão "sobre o conceito de imagem estar correto .Imagem é ,para todo elemento no contradomínio existe pelo menos um associado a um ou mais elementos no domínio .Há casos que diferentes valores no domínio estar associado a um mesmo elemento no CD .
Não necessariamente. Note que podemos definir

com

. Note que existem infinitos elementos no contradomínio para os quais não há qualquer elemento do domínio associando-o. Agora, obrigatoriamente na imagem temos cada elemento sendo associado por um elemento no domínio.
Conclusão: contradomínio e imagem não necessariamente são o mesmo conjunto, somente quando definimos a função de tal maneira que esta seja sobrejetora (escolhendo o contradomínio como igual a imagem). Note que a imagem sempre deve estar contida no contradomínio.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Sex Ago 03, 2012 11:27
por e8group » Sex Ago 03, 2012 11:27
É verdade ,mas foi exatamente isso que eu disse (talvez não ficou tão claro ) .
Para todo elemento no contradomínio existe pelo menos um elemento (do contradomínio) associado a um ou mais elementos no domínio .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sex Ago 03, 2012 12:26
por MarceloFantini » Sex Ago 03, 2012 12:26
Novamente, na primeira parte grifada você quis dizer para todo elemento na imagem?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Sex Ago 03, 2012 13:15
por e8group » Sex Ago 03, 2012 13:15
Boa tarde Marcelo Fantini , oque eu quis dizer matematicamente foi ,
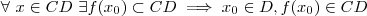
Certo ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Sex Ago 03, 2012 13:36
por MarceloFantini » Sex Ago 03, 2012 13:36
Seus símbolos dizem o seguinte: para todo elemento do contradomínio existe a imagem de um elemento contida (?) no contradomínio, que implica que existe um elemento do domínio tal que a imagem desse elemento pertence ao contradomínio.
Continua sem sentido. Até agora, o que você afirma é que todo elemento do contradomínio tem um elemento do domínio associado, o que é falso a menos que a função seja sobrejetora. Se você discorda, mostre um elemento associado a -1 para

,

como acima. A afirmação "para todo elemento do contradomínio existe pelo menos um elemento do contradomínio associado a um ou mais elementos do domínio" não tem sentido matemático.
Acho que o que você quer dizer é: para todo elemento

na imagem, contida no contradomínio, existe um elemento

do domínio tal que
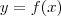
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Sex Ago 03, 2012 14:03
por e8group » Sex Ago 03, 2012 14:03
Ok ! Grato .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funçao modular
por Fiel8 » Sex Jul 10, 2009 19:25
- 1 Respostas
- 2622 Exibições
- Última mensagem por Molina

Sex Jul 10, 2009 21:50
Funções
-
- Função Modular
 por geriane » Sáb Abr 03, 2010 21:32
por geriane » Sáb Abr 03, 2010 21:32
- 3 Respostas
- 3122 Exibições
- Última mensagem por Molina

Dom Abr 04, 2010 12:57
Funções
-
- Funçao modular
 por Skcedas » Qua Mai 26, 2010 19:29
por Skcedas » Qua Mai 26, 2010 19:29
- 6 Respostas
- 5381 Exibições
- Última mensagem por netlopes

Ter Jun 08, 2010 18:11
Funções
-
- Função Modular
 por DanieldeLucena » Seg Set 20, 2010 18:03
por DanieldeLucena » Seg Set 20, 2010 18:03
- 1 Respostas
- 2253 Exibições
- Última mensagem por MarceloFantini

Seg Set 20, 2010 19:35
Funções
-
- Função Modular
por Pri Ferreira » Ter Nov 22, 2011 18:20
- 1 Respostas
- 1879 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 18:56
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


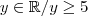 isto é a imagem da função modular é maior ou igual a 5 para domínio real ,em outras palavras ,
isto é a imagem da função modular é maior ou igual a 5 para domínio real ,em outras palavras ,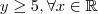

 com
com  . Note que existem infinitos elementos no contradomínio para os quais não há qualquer elemento do domínio associando-o. Agora, obrigatoriamente na imagem temos cada elemento sendo associado por um elemento no domínio.
. Note que existem infinitos elementos no contradomínio para os quais não há qualquer elemento do domínio associando-o. Agora, obrigatoriamente na imagem temos cada elemento sendo associado por um elemento no domínio. 

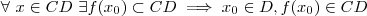
 na imagem, contida no contradomínio, existe um elemento
na imagem, contida no contradomínio, existe um elemento  do domínio tal que
do domínio tal que 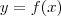 .
.