Boa tarde! Não sei se estou entendendo errado a idéia de imagem, mas, tentei fazer uma função modular do tipo:
I 3x - 1 I - 5, definida em R cujo valor de f é (1/3) e (-1/3). Eu encontrei os valores -5 e -3. O problema passou a surgir quando ele me perguntou o conjunto imagem dessa função. Pelo que eu entendo de conjunto imagem significa o reflexo dos valores que você atribui a X substituindo na equação tais valores e encontra o seu resultado. Nessa questão eu usei valores imaginários de -2,-1,0,1,2 e pensei que seus resultados na equação fossem a sua imagem. O livro diz que o conjunto imagem dessa questão é {y E R/y>ou igual a 5}. Ele admite valores maiores ou iguais a 5 e somente 5, por que?


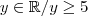 isto é a imagem da função modular é maior ou igual a 5 para domínio real ,em outras palavras ,
isto é a imagem da função modular é maior ou igual a 5 para domínio real ,em outras palavras ,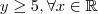

 com
com  . Note que existem infinitos elementos no contradomínio para os quais não há qualquer elemento do domínio associando-o. Agora, obrigatoriamente na imagem temos cada elemento sendo associado por um elemento no domínio.
. Note que existem infinitos elementos no contradomínio para os quais não há qualquer elemento do domínio associando-o. Agora, obrigatoriamente na imagem temos cada elemento sendo associado por um elemento no domínio. 

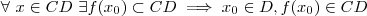
 na imagem, contida no contradomínio, existe um elemento
na imagem, contida no contradomínio, existe um elemento  do domínio tal que
do domínio tal que 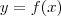 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)