Teve uma equação que eu não consegui resolver sem antes ter olhado a resposta no gabarito e te-la desmontado de trás para frente
lnx +ln(x-1)=1
Resposta
![\frac{1}{2}\left(1+\sqrt[]{1+4e} \right) \frac{1}{2}\left(1+\sqrt[]{1+4e} \right)](/latexrender/pictures/d0f1f618f595c54d9e155b6a586d36ba.png)
A minha equação só chegava até aqui
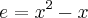
Resolvendo a resposta de trás pra frente eu percebo que o primeiro passo foi multiplicar por 4 os membros da equação
![2x=1+\sqrt[]{1+4e} 2x=1+\sqrt[]{1+4e}](/latexrender/pictures/9a4c1e5bd7d9c16319accad6b8ffa4cb.png)
![2x-1=\sqrt[]{1+4e} 2x-1=\sqrt[]{1+4e}](/latexrender/pictures/cfa8e77731de655ce1e97dbae30c1852.png)
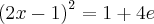
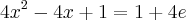
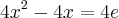
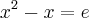
Bom, quero saber porque esse foi o primeiro passo. Depois que a conta ta pronta eu vi lógica mas antes disso eu não entendi por que. Como saber disso. Alguém pode resolver esta questão explicando cada linha na ordem correta? Tipo tinha que achar algum número que multiplicado com a equação fosse possível formar o quadrado perfeito?
Agradeço desde já a quem me ajudar a entender!


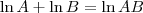
![\ln x + \ln (x-1) = \ln [x(x-1)]=\ln(x^2-x) \ln x + \ln (x-1) = \ln [x(x-1)]=\ln(x^2-x)](/latexrender/pictures/a7b5be83c9810910969cc35547478f25.png)
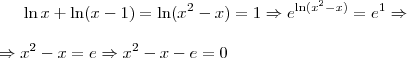
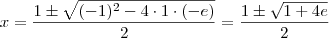
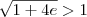 , devemos somente considerar o valor positivo, ou seja,
, devemos somente considerar o valor positivo, ou seja,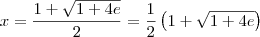


 .
.
 :
: