 por apcsrs » Qui Jan 05, 2012 10:17
por apcsrs » Qui Jan 05, 2012 10:17
Olá,
Sempre me foi ensinado que em todas as ocasiões possíveis eu deveria simplificar as equações, não sendo apresentadas para mim restrições a isso.
No entanto, há alguns dias foi me apresentado uma equação em que, simplificando, havia perda de uma resposta da equação, como no caso:

No entanto, ao resolver um exercício hoje pela manhã, me deparei com:
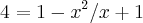
, onde a resolução se fazia por meio de simplificação.
Minha dúvida consiste em saber quando posso simplificar uma equação e quando não posso.
Obrigado.
-
apcsrs
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jan 05, 2012 10:01
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Fisica
- Andamento: cursando
 por fraol » Qui Jan 05, 2012 16:10
por fraol » Qui Jan 05, 2012 16:10
Olá,
Em matemática elementar, no universo dos números reais, as restrições que você deve considerar são os casos da divisão por zero e da raiz de número negativo.
Na sua expressão:

a simplificação é feita mediante a divisão de ambos os lados da equação por
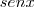
. Então a restrição aqui é de que
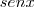
não pode ser igual 0, isto é o ângulo

deve ser diferente de
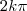
para
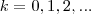
.
A mesma restrição ocorre na segunda expressão, pois temos uma divisão por

.
Não entendi o trecho
... simplificando, havia perda de uma resposta da equação, ...
.
Se você puder explicar um pouco mais seria bom ...
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por apcsrs » Qui Jan 05, 2012 16:19
por apcsrs » Qui Jan 05, 2012 16:19
Cara, você conseguiu me dar uma idéia.
No caso do senx era extamente essa a questão, pois anulando o sen x, anularia K2pi...
Obrigado
Fica com Deus
-
apcsrs
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jan 05, 2012 10:01
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Fisica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- simplificação de equações do segundo grau
por damasobh » Dom Mar 27, 2011 23:44
- 3 Respostas
- 7366 Exibições
- Última mensagem por MarceloFantini

Qua Abr 20, 2011 13:10
Sistemas de Equações
-
- [Equações exponenciais] Ajuda com simplificação
por stilobreak » Qua Mar 20, 2013 03:15
- 3 Respostas
- 4300 Exibições
- Última mensagem por DanielFerreira

Dom Mar 24, 2013 19:35
Equações
-
- Duvida em simplificacao
por bmachado » Seg Abr 30, 2012 17:21
- 2 Respostas
- 1419 Exibições
- Última mensagem por bmachado

Ter Mai 01, 2012 15:31
Álgebra Elementar
-
- duvida em simplificacao
por bmachado » Qua Mai 02, 2012 16:47
- 1 Respostas
- 1215 Exibições
- Última mensagem por bmachado

Qua Mai 02, 2012 16:57
Álgebra Elementar
-
- Duvida Simplificação - [RESOLVIDO]
por Peregrinu » Sáb Abr 14, 2012 21:30
- 6 Respostas
- 2772 Exibições
- Última mensagem por DanielFerreira

Dom Abr 15, 2012 13:19
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

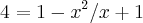 , onde a resolução se fazia por meio de simplificação.
, onde a resolução se fazia por meio de simplificação.


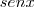 . Então a restrição aqui é de que
. Então a restrição aqui é de que  deve ser diferente de
deve ser diferente de 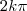 para
para 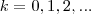 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  .
.
